Generic Quadratic Formula
We learnt how to factorise and solve basic quadratic equations . The method shown earlier can be used for solving quadratic equations with real roots.
However there can be quadratic equations with irrational or even imaginary roots. The earlier method cannot be applied in those cases.
Today we will learn a new method to solve quadratic equations which can be applied to equations having any types of roots, including irrational or imaginary ones.
I. Introduction To Quadratic Expression
A quadratic expression is of the form $ax^2 + bx + c$, where the highest power of $x$ is $2$. If we compute the values of this expression at various values of $x$ and consider the result as $y$, we can write this as:
$y = ax^2 + bx + c$
Now, if we plot different values of $y$ with the corresponding values of $x$, we will get a shape which will look like:
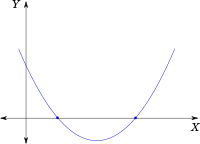 or
or 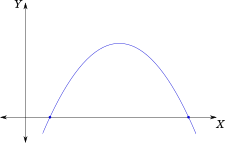
depending on whether $a$ is positive or negative.
-----------book page break-----------
Try the widget below and observe how the roots are changing as you change the shape and position of the curve.
Observe the following:
There is no real root for a quadratic equation when the corresponding quadratic function lies
completely on one side of the $x-axis$
. That is there is no intersection point of the curve and the $x-axis$
.There is exactly one root of the equation when the $x-axis$ is
a tangent to
the curve.The curve opens upwards when the value of $a$ is
positive
and opens downwards when the value of $a$ is negative
.-----------book page break-----------
II. Roots Of Quadratic Equation
Let us start with the generic form of quadratic equation, which is:
$ax^2 + bx + c = 0$ where $a$, $b$ and $c$ are constants and $a \ne 0$, because if $a$ is $0$ then this is not a quadratic equation.
$ax^2 + bx + c = 0$ ...dividing both sides by $a$ we get,
$\dfrac{ax^2 + bx + c}{a} = \dfrac{0}{a}$
$\Rightarrow \dfrac{ax^2}{a} + \dfrac{bx}{a} + \dfrac{c}{a} = 0$
$\Rightarrow x^2 + \dfrac{bx}{a} + \dfrac{c}{a} = 0$
$\Rightarrow x^2 + \dfrac{b}{a}x + \dfrac{c}{a} = 0$
$\Rightarrow x^2 + \dfrac{b}{a}x = - \dfrac{c}{a}$ ... now adding $\left(\dfrac{b}{2a}\right)^2$ to both sides of the equation, we get,
$x^2 + \dfrac{b}{a}x + \left(\dfrac{b}{2a}\right)^2 = - \dfrac{c}{a} + \left(\dfrac{b}{2a}\right)^2$ ... now rewriting the term $\dfrac{b}{a}x$ as $2\cdot x \cdot \dfrac{b}{2a}$ we get:
$x^2 + 2\cdot x \cdot \dfrac{b}{2a} + \left(\dfrac{b}{2a}\right)^2 = - \dfrac{c}{a} + \dfrac{b^2}{4a^2}$
$\Rightarrow x^2 + 2\cdot x \cdot \dfrac{b}{2a} + \left(\dfrac{b}{2a}\right)^2 = \dfrac{b^2}{4a^2} - \dfrac{c}{a}$
-----------book page break-----------
$\Rightarrow x^2 + 2\cdot x \cdot \dfrac{b}{2a} + \left(\dfrac{b}{2a}\right)^2 = \dfrac{b^2}{4a^2} - \dfrac{4ac}{a^2}$
$\Rightarrow x^2 + 2\cdot x \cdot \dfrac{b}{2a} + \left(\dfrac{b}{2a}\right)^2 = \dfrac{b^2 - 4ac}{4a^2}$
Now we can see that the left hand side of the equation is of the form
$(a + b)^2$
, therefore, we can write:$\left(x + \dfrac{b}{2a}\right)^2 = \dfrac{b^2 - 4ac}{4a^2}$
Next, taking square roots of both sides, we get:
$x + \dfrac{b}{2a} = \pm \sqrt{\dfrac{b^2 - 4ac}{4a^2}} = \pm \dfrac{\sqrt{b^2 - 4ac}}{\sqrt{4a^2}} = \pm \dfrac{\sqrt{b^2 - 4ac}}{2a}$ ... observe that we have considered both positive and negative square roots
$\Rightarrow x = - \dfrac{b}{2a} \pm \dfrac{\sqrt{b^2 - 4ac}}{2a}$
$\Rightarrow x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$
We know that a quadratic equation will have two roots, except when the quadratic expression is a perfect square. In our case, we obtain the two roots by splitting the $\pm$ symbol into, $+$ and $-$ cases respectively.
Hence our two roots become:
$\Rightarrow x = \dfrac{-b + \sqrt{b^2 - 4ac}}{2a}$, and,
$\Rightarrow x = \dfrac{-b - \sqrt{b^2 - 4ac}}{2a}$
-----------book page break-----------
Now we will take a closer look at the term $\sqrt{b^2 - 4ac}$. As you can see, that this term is the one which makes the two roots different, therefore this term is called the $\unicode{0x201C}discriminant\unicode{0x201D}$
Now we can consider a few cases based on the discriminant:
$\underline{Case\ 1:}$
$b^2 - 4ac = 0$, in this case our quadratic expression is a perfect square and there is only one root.
$\underline{Case 2:}$
$b^2 - 4ac$ is a perfect square. In this case both the numerator and the denominator are integers, hence we will get rational roots.
$\underline{Case 3:}$
$b^2 - 4ac$ is positive but not a perfect square. In this case the numerator is an irrational number, while the denominator is an integer, hence both roots will be irrational numbers.
$\underline{Case 4:}$
$b^2 - 4ac$ is a negative number. We know that conventionally square roots of negative numbers do not exist. So, what we end up getting in this case are called complex roots. We will learn more about complex numbers when we cover imaginary numbers.
III. Sum & Product Of Roots
Now that we know the general form of the roots of a quadratic equation, let us see what will be their sum and products.
-----------book page break-----------
Let two roots be:
$\alpha = \dfrac{-b + \sqrt{b^2 - 4ac}}{2a}$
$\beta = \dfrac{-b - \sqrt{b^2 - 4ac}}{2a}$
$\therefore \alpha + \beta = \dfrac{-b + \sqrt{b^2 - 4ac}}{2a} + \dfrac{-b - \sqrt{b^2 - 4ac}}{2a}$
$\Rightarrow \alpha + \beta = \dfrac{-b + \sqrt{b^2 - 4ac} -b - \sqrt{b^2 - 4ac}}{2a} = \dfrac{-2b}{2a} = -\dfrac{b}{a}$
Similarly the product of the two roots can be computed in the following way:
$\alpha \cdot \beta = \left(\dfrac{-b + \sqrt{b^2 - 4ac}}{2a}\right)\left(\dfrac{-b - \sqrt{b^2 - 4ac}}{2a}\right)$
$\Rightarrow \alpha \cdot \beta = \dfrac{\left(-b + \sqrt{b^2 - 4ac}\right)\left(-b - \sqrt{b^2 - 4ac}\right)}{4a^2}$
$\Rightarrow \alpha \cdot \beta = \dfrac{(-b)^2 - \left(\sqrt{b^2 - 4ac}\right)^2}{4a^2}$
$\Rightarrow \alpha \cdot \beta = \dfrac{b^2 - \left(b^2 - 4ac\right)}{4a^2}$
$\Rightarrow \alpha \cdot \beta = \dfrac{b^2 - b^2 + 4ac}{4a^2} = \dfrac{4ac}{4a^2} = \dfrac{c}{a}$
-----------book page break-----------
IV. Maximum And Minimum Value Of A Quadratic Expression
Now that we have a good understanding of the shape of a quadratic function from Section I, we know that when we plot the value of $x$ and $y$ the $y$ value for a particular curve has either a
minimum value
or a maximum value
but not both.The maximum value or the minimum value is always at the vertex of the curve. In this section we will look at two different methods of understanding maxima/minima of a quadratic expression, the first one being a visual approach using symmetry, while the second one is the formal derivation.
Visual Approach:
The following diagram shows the plot of a quadratic function with a positive $a$.
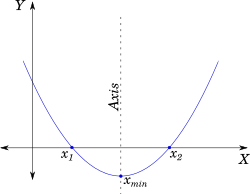
Let's say this function has a minimum value at $x = x_{min}$.
This is the vertex of the parabola shown in the figure, and the line passing through the vertex, parallel to the $Y-axis$ is called the axis of the parabola. A parabola is symmetric about this axis.
If we consider the two roots as $x_1$ and $x_2$, then the $X$ value of the vertex, $x_{min}$ is the same as the midpoint of $x_1x_2$.
-----------book page break-----------
Therefore, we get:
$x_{min} = (x_1 + x_2)/2$
Since the two roots are given by $\dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a}$, we get:
$x_{min} = \left. \left( \dfrac{-b + \sqrt{b^2 - 4ac}}{2a} + \dfrac{-b - \sqrt{b^2 - 4ac}}{2a} \right) \middle/ 2\right.$
$x_{min} = \left. \left( \dfrac{-2b}{2a} \right) \middle/ 2\right.$
$x_{min} = \dfrac{-b}{2a}$
Notice that in case of complex roots, there is no visible root, but the above relation still holds because while adding the two roots, the complex parts $\pm \sqrt{b^2 - 4ac}$ still cancel out, leaving us with $\dfrac{-b}{2a}$
Formal Derivation:
Given any generic quadratic expression $ax^2 + bx + c$ we can express it as follows:
$ax^2 + bx + c$
$= a\left(x^2 + \dfrac{bx}{a} + \dfrac{c}{a} \right)$
$= a\left[x^2 + 2 \cdot \dfrac{b}{2a} \cdot x + \left(\dfrac{b}{2a} \right)^2 - \left(\dfrac{b}{2a} \right)^2 + \dfrac{c}{a} \right]$
$= a\left[ \left(x + \dfrac{b}{2a} \right)^2 + \dfrac{c}{a} - \left(\dfrac{b}{2a} \right)^2 \right]$
-----------book page break-----------
Now observe that $\left(x + \dfrac{b}{2a} \right)^2$ is a non-negative quantity, and the rest of the term is independent of $x$, that is, they are constant.
Therefore, the minimum value of the expression inside the square braces is obtained when we have:
$\left(x + \dfrac{b}{2a} \right)^2 = 0$
$\Rightarrow x = \dfrac{-b}{2a}$
Now, if $a$ is positive, minimizing the inside quantity will give us the minimum value of the whole expression, while, if $a$ is negative, then minimizing the expression inside will give us the
maximum value
of the whole expression. In both cases this is obtained by assigning $x = \dfrac{-b}{2a}$.