Slope Of Perpendicular Lines

Today we are going to understand an important property of the slopes of lines that are perpendicular to each other.

To understand this better, we need to be able to visualise slope as a trigonometric ratio.

we learnt about slope as a ratio of the vertical and horizontal distance between any two points.

Let us consider the lines $AB$ and $CD$, intersecting each other at $M$ at right angle, and neither is parallel to any of the axes, as shown in the figure below:

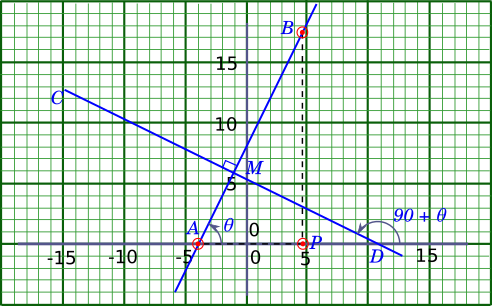
-----------book page break-----------

Let us first consider line $AB$. We know from the definition of slope that:

$slope = \dfrac{PB}{AP}$

Let us say this line makes an angle of magnitude $\theta$ with the positive $X$ axis. Since $\triangle APB$ is right angled, we know from our definitions of trigonometric ratios, that $\dfrac{PB}{AP} = tan(\theta)$.

Hence, another definition of slope is as follows:

$The\ slope\ of\ a\ line\ is\ the\ tangent\ of\ the\ angle\ it\ makes\ $$with\ the\ positive\ X\ axis$

Now since, $CD$ is perpendicular to $AB$, if we consider $\triangle AMD$, external $\angle D = 90 + \theta$

This is the angle that $CD$ makes with the positive $X$ axis.

Therefore, slope of line $CD$ is $tan(90 + \theta)$

We know from our knowledge of trigonometric ratios in different quadrants and their relationships that:

$tan(90 + \theta) = -cot(\theta)$

$\therefore slopeAB \times slopeCD = tan(\theta) \times \{-cot(\theta)\}$

$= -tan(\theta) \times \dfrac{1}{tan(\theta)}$

$= -1$

Hence, we can say that the product of the slopes of a pair of perpendicular lines, that are not parallel to any of the axes, is equal to $-1$.