Understanding The Parabola
I. Introduction
we saw that when the eccentricity, $e$, of a conic section become equal to $1$, it forms a parabola. It has some important geometric properties which makes it suitable for various applications like telescopes, automobile headlight reflectors, tracing projectile path, etc.
II. Derivation
The parabola can be defined using the concept of locus as follows:
It is the locus of a point whose distance from a fixed straight line (directrix) is equal to its distance from a fixed point (focus).
To derive the standard form of parabola we will choose the axes of our Cartesian plane such that the directrix is parallel to the $y$-axis and the focus lies on the $x$-axis.
Therefore, the equation of the directrix is $x = d$ and the focus $F = (f, 0)$
If we choose any random point $P = (x, y)$ on the parabola, then its distance from the directrix is:
$x - d$ and its distance from the focus is $\sqrt{(x - f)^2 + (y - 0)^2} = \sqrt{(x - f)^2 + y^2}$ as shown in the following figure:
-----------book page break-----------
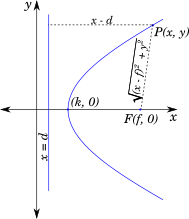
Based on the definition of parabola, the two distances are equal, therefore,
$x - d = \sqrt{(x - f)^2 + y^2}$
$\Rightarrow (x - d)^2 = (x - f)^2 + y^2$
$\Rightarrow \cancel{x^2} - 2dx + d^2 = \cancel{x^2} - 2xf + f^2 + y^2$
$\Rightarrow y^2 = 2x(f - d) + d^2 - f^2$
$\Rightarrow y^2 = 2x(f - d) + (d-f)(d+f)$
$\Rightarrow y^2 = 2(f - d)x - (f - d)(d+f)$
Now, let's say the graph intersects the $x$-axis at point $(k, 0)$. Substituting $y = 0$ and $x = k$ in the above equation we get:
$0^2 = 2(f - d)k - (f - d)(f + d)$
-----------book page break-----------
$\Rightarrow (f - d)\left\{2k - (f + d)\right\} = 0$
$\because$ the focus does not lie on the directrix, $f \ne d$
$\therefore 2k = (f + d)$
$\Rightarrow k = \dfrac{f + d}{2}$
Therefore, the equation of the parabola becomes:
$y^2 = 2(f - d)x - 2(f - d)k$
Since $f$ and $d$ are also constants we can substitute $(f - d) = 2a$ where $a$ is a constant and $a \ne 0$ and get the equation as:
$y^2 = 4a(x - k)$
Notice, if the parabola passes through the origin, we will get $k = 0$, by substituting $x = 0, y = 0$ in the above equation. Which gives the equation as:
$y^2 = 4ax$
Observe that we took the directrix as parallel to the $y$-axis that is why we got the parabola as symmetric about the $x$-axis. Had we taken the directrix as parallel to the $x$-axis and the focus on the $y$-axis, we would have gotten an equation of the form:
$x^2 = 2a(y - k)$ which would have been symmetric about the $y$-axis.
-----------book page break-----------
You can experiment with the widget shown below to familiarize yourself with parabola with different directrix and the focus.
III. Properties Of Parabola
Latus Rectum:
It is the line segment parallel to the directrix, passing through the focus and terminated at both ends by the parabola.
If we take the equation of the parabola as $y^2 = 4a(x - k)$, then the Latus Rectum is of length $4a$.
We saw in the derivation given in the previous section that in this standard form, the focus is at $(f, 0)$, and
$2a = f - d$
$2k = f + d$
Therefore, $f = a + k$
-----------book page break-----------
Since the latus rectum is a line parallel to the directrix ($y$-axis, in this case), passing through the focus, its equation is $x = a + k$
To find the two intersection point with the parabola we substitute $x = a + k$ in our equation of the parabola and obtain:
$y^2 = 4a(a + k - k)$
$\Rightarrow y^2 = 4a^2$
$\Rightarrow y = \pm 2a$
Therefore, the intersection points of the latus rectum with the parabola are $(a + k, 2a)$ and $(a + k, -2a)$.
The length of the latus rectum is, therefore, $2a - (-2a) = 4a$
Reflective Property:
Any light ray parallel to the axis of the parabola, after being reflected off the inner surface of the parabola passes through the focus of the parabola.
This property also implies that the tangent at any point, $P$, on the parabola bisects the angle formed by the lines joining $P$ with the focus and the perpendicular from $P$ to the directrix.
Tangents Drawn From The Directrix:
Two tangents drawn to a parabola from any point on the directrix are perpendicular to each other. Conversely, if two tangents drawn to a parabola are perpendicular to each other, their intersection point lies on the directrix.
-----------book page break-----------
IV. Properties Of Tangents To A Parabola
If we have a line of the form $y = mx + c$ is a tangent to a given parabola of the form $y^2 = 4ax$, then
$c = \dfrac{a}{m}$
Proof:
Let the line $y = mx + c$ be a tangent to the parabola $y^2 = 4ax$ at a point $x_1, y_1$.
Since the point lies on the parabola ${y_1}^2 = 4ax_1$
Since the point lies on the tangent $y_1 = mx_1 + c$
Therefore,
$(mx_1 + c)^2 = 4ax_1$
$\Rightarrow m^2{x_1}^2 + 2mcx_1 + c^2 - 4ax_1 = 0$
$\Rightarrow m^2{x_1}^2 + 2(mc - 2a) x_1 + c^2 = 0$
Since the tangent touches the parabola at a single point, the above quadratic equation has exactly one solution and its discriminant is $0$
Therefore,
$4(mc - 2a)^2 - 4m^2c^2 = 0$
$\Rightarrow (mc - 2a)^2 - m^2c^2 = 0$
$\Rightarrow \cancel{m^2c^2} - 4amc + 4a^2 - \cancel{m^2c^2} = 0$
$\Rightarrow amc = a^2$
$\Rightarrow c = \dfrac{a}{m}$