Introduction To Venn Diagram

Venn diagrams, named after John Venn, give us an easy way to represent and view Sets and their relationships. They are also known as Set diagram, Primary diagram or Logic diagram.

Venn diagrams use closed shapes (usually circles/ellipses) to represent sets. They can very easily denote overlaps between various logical groups.

Let us say the we define the following sets:

$Set\ A$: The set of all prime numbers between $1$ and $10$. Therefore set $A$ will contain the elements

$2$, $3$, $5$ and $7$

$Set\ B$: The set of all even numbers between $1$ and $10$. Therefore set $B$ will contain the elements $2$, $4$, $6$, $8$ and $10$.

$Set\ C$: The set of all odd numbers between $1$ and $10$. Therefore set $C$ will contain the elements $1$, $3$, $5$, $7$ and $9$.

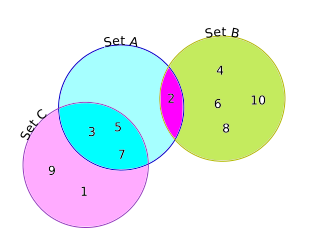
If we were to draw the Venn diagram for these sets, we would draw the following diagram:

Note that since there is no number that is both odd as well as even. So the diagram does not contain an overlap between Set B and Set C.

Now let us look at the regions marked by various colors and what they mean.

Color	What They Mean
	This region is the overlap between set $A$ and set $C$, which means it contains all the elements that are prime and are odd. Therefore it contains $3$, $5$ and $7$
	This region is the overlap between Set $A$ and Set $B$, which means it contains all elements that are prime and are even. The only such number is $2$.
	This region contains elements that are elements of Set $C$ but are not part of Set $A$ or Set $B$, that is numbers that are odd and neither prime or even. The only numbers between $1$ and $10$, that satisfy these conditions are $1$ and $9$.
	This region should contain all elements that are prime but neither even nor odd. There is no such number which is neither even nor odd, therefore this region is empty.
	This region indicates elements that are even but not prime nor odd. The elements that satisfy these conditions are $4$, $6$, $8$ and $10$.

Now the Venn Diagram in our example contains much more details than are provided in actual Venn diagrams. Usually sets contain a large number of elements, hence, it is not practical to show the actual elements. In most Venn Diagrams only the set names and their relationships are shown. For example, the above Venn diagram will be drawn like below. The set definition should be mentioned clearly before drawing the Venn diagram.