Area Of Closed Polygon

$\underline{I.\ Theory}$

If we define a closed, $n$-sided polygon on the Cartesian plane, using the points $(x_1,y_2),\ (x_2,y_2),\ (x_3,y_3),\ ...\ (x_n,y_n)$, taken in order, as vertices its area can be determined using the absolute value of:

$\dfrac{1}{2}\{x_1(y_n - y_2) + x_2(y_1 - y_3) + x_3(y_2 - y_4) + ... + x_n(y_{n-1} - y_1)\}$

$\underline{II.\ Derivation}$

We will understand this by understanding the derivation for a generic quadrilateral $(n = 4)$ and extending the same for other polygons.

In the following diagram, $P_1P_2P_3P_4$ is a quadrilateral drawn on a Cartesian plane.

Lines $P_1Q_1$, $P_2Q_2$, $P_3Q_3$ and $P_4Q_4$ are drawn from the respective vertices to the $X$ axis.

-----------book page break-----------

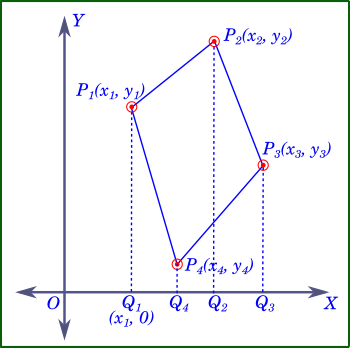
The area of $P_1P_2P_3P_4$ can be found by using:

$ar[P_1P_2P_3P_4] = ar[P_1P_2Q_2Q_1] + ar[P_2P_3Q_3Q_2]$$\qquad \qquad - ar[P_4P_3Q_3Q_4] - ar[P_1P_4Q_4Q_1]$

$P_1P_2Q_2Q_1$ is a trapezium with $P_1Q_1 \parallel P_2Q_2$ and $Q_1Q_2$ as the height.

$\therefore ar[P_1P_2Q_2Q_1] = \dfrac{1}{2}[(x_2 - x_1)(y_2 + y_1)] = \dfrac{1}{2}[x_2y_2 + x_2y_1 - x_1y_2 - x_1y_1]$

-----------book page break-----------

Similarly,

$ar[P_2P_3Q_3Q_2] = \dfrac{1}{2}[(x_3 - x_2)(y_2 + y_3)] = \dfrac{1}{2}[x_3y_2 + x_3y_3 - x_2y_2 - x_2y_3]$

$ar[P_4P_3Q_3Q_4] = \dfrac{1}{2}[(x_3 - x_4)(y_3 + y_4)] = \dfrac{1}{2}[x_3y_3 + x_3y_4 - x_4y_3 - x_4y_4]$

$ar[P_1P_4Q_4Q_1] = \dfrac{1}{2}[(x_4 - x_1)(y_4 + y_1)] = \dfrac{1}{2}[x_4y_4 + x_4y_1 - x_1y_4 - x_1y_1]$

Therefore,

$ar[P_1P_2P_3P_4]$

$= \dfrac{1}{2}[(x_2 - x_1)(y_2 + y_1)] + \dfrac{1}{2}[(x_3 - x_2)(y_2 + y_3)]$ $\qquad - \dfrac{1}{2}[(x_3 - x_4)(y_3 + y_4)] - \dfrac{1}{2}[(x_4 - x_1)(y_4 + y_1)]$

$= \dfrac{1}{2}[(x_2 - x_1)(y_2 + y_1) + (x_3 - x_2)(y_2 + y_3)$ $\qquad - (x_3 - x_4)(y_3 + y_4) - (x_4 - x_1)(y_4 + y_1)]$

$= \dfrac{1}{2}[(x_2 - x_1)(y_2 + y_1) + (x_3 - x_2)(y_2 + y_3)$ $\qquad + (x_4 - x_3)(y_3 + y_4) + (x_1 - x_4)(y_4 + y_1)]$

$= \dfrac{1}{2}[\cancel{x_2y_2} + x_2y_1 - x_1y_2 - \cancel{x_1y_1} + x_3y_2 + \cancel{x_3y_3} - \cancel{x_2y_2} - x_2y_3$ $\qquad + x_4y_3 + \cancel{x_4y_4} - \cancel{x_3y_3} - x_3y_4 - \cancel{x_4y_4} - x_4y_1 + x_1y_4 + \cancel{x_1y_1}]$

$=$ $\dfrac{1}{2}[x_2y_1 - x_1y_2 + x_3y_2 - x_2y_3 + x_4y_3 - x_3y_4 - x_4y_1 + x_1y_4]$ $\qquad ...(i)$

$= \dfrac{1}{2}[x_1(y_4 - y_2) + x_2(y_1 - y_3) + x_3(y_2 - y_4) + x_4(y_3 - y_1)]$

-----------book page break-----------

$\underline{III.\ Important\ Observations}$

Now, let us make some important observations about this formula.

We are taking the $X$ coordinate of each point multiplied by the $Y$ coordinate of the previous point minus the $Y$ coordinate of the next point.

Adding all these terms, and multiplying by $\dfrac{1}{2}$ we get the area of the polygon.

We are considering the points starting with any point and going in clockwise direction. Had we considered the points in anti-clockwise direction we would have ended up with the value:

$\dfrac{1}{2}[x_1(y_2 - y_4) + x_2(y_3 - y_1) + x_3(y_4 - y_2) + x_4(y_1 - y_3)]$

$= (-1) \times \dfrac{1}{2}[x_1(y_4 - y_2) + x_2(y_1 - y_3) + x_3(y_2 - y_4) + x_4(y_3 - y_1)]$

Depending on the choice of the first point and the direction you choose, you can get a $-ve$ value for the area, therefore, you must consider the absolute value of the final answer that you get.

What would we get if we did the same derivation, but this time using the $Y$ axis to draw the trapeziums? Since the area of the trapezium will not change, therefore, we should get the same result.

As a matter of fact we can re-write expression $(i)$ as:

$\dfrac{1}{2}[x_2y_1 - x_1y_2 + x_3y_2 - x_2y_3 + x_4y_3 - x_3y_4 - x_4y_1 + x_1y_4]$

$= \dfrac{1}{2}[y_1(x_2 - x_4) + y_2(x_3 - x_1) + y_3(x_4 - x_2) + y_4(x_1 - x_3)]$