Angles Formed By Intersecting Lines

I. Introduction

Previously we saw the related to angles. In this chapter we will see some more important properties of lines and angles.

Specifically we will see how the angles formed by two intersecting lines are related to each other. We will also see how proofs in mathematics work.

II. Problem Description

When two straight lines intersect as shown below, we get four angles, formed at the point of intersection as shown in the diagram below:

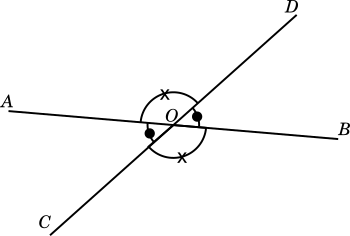
$\text{Figure - 1}$

-----------book page break-----------

$\text{Figure - 1}$ shows the lines $AB$ and $CD$ intersecting at point $O$ forming $\angle AOC$ (marked with $\unicode{0x2B24}$), $\angle COB$ (marked with $\unicode{0x2716}$), $\angle BOD$ (marked with $\unicode{0x2B24}$) and $\angle DOA$ (marked with $\unicode{0x2716}$)

In the above figure any two angles which are adjacent to each other, that is, one marked with a $\unicode{0x2B24}$ and the other with a $\unicode{0x2716}$ and share a common arm are called supplementary angles. They always sum up to a

straight angle

$180^o$

As we can see from the given diagram there are four pairs of supplementary angles, which are:

$\angle AOD$, $\angle DOB$,

$\angle DOB$, $\angle BOC$

$\angle BOC$, $\angle COA$

$\angle COA$, $\angle AOD$

The angles that do not share a common arm and only have point $O$ as the common point are called the vertically opposite angles. There are two pairs of vertically opposite angles, which are:

$\angle AOC\ and\ \angle BOD$

$\angle AOD\ and\ \angle BOC$

It is easy to understand that the vertically opposite angles are equal.

In $\text{Figure - 1}$

$\angle AOD + \angle AOC = 180^o$ and

$\angle AOD + \angle BOD = 180^o$

We can see that adding either $\angle AOC$ or $\angle BOD$ to $\angle AOD$ gives the same result of $180^o$.

Therefore, $\angle AOC$ must be equal to $\angle BOD$. Thus vertically opposite angles are equal.

Angle Definitions -