Asymptotes
The understanding of this chapter depends largely on your understanding of the concept of limits, which you can find .
I. Understanding Asymptotes
A straight line of the form $ax + by + c = 0$ is called an asymptote to any given curve $y = f(x)$ if the distance between the line and the curve approaches $0$ as $x$ or $f(x)$ approaches $+\infty$ or $-\infty$
Let us understand the concept of asymptotes with an example. The following is the plot of the funciton:
$y = \dfrac{1}{x}$ or $xy = 1$
Let us observe certain properties of the plot.
- The $y$ value reaches almost $0$ as $x$ grows very large either in the positive or negative direction.
- Since, when $x$ is positive, $y$ is also positive and vice versa for negative $x$, the two parts of the curve are restricted purely to the first and the third quadrant. No part of the curve is present in the second or the fourth quadrant, where $x$ and $y$ are of opposite signs.
- The behaviour of the curve is exactly same with respect to the $y$-axis, as $y$ grows very large in the positive or negative direction.
The $x$-axis is the horizontal asymptote and the $y$-axis is the vertical asymptote of this curve.
-----------book page break-----------
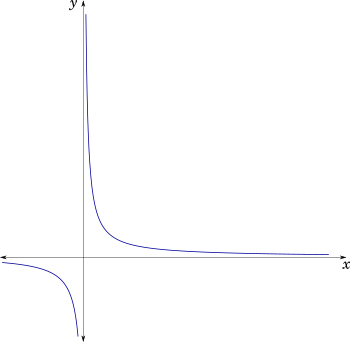
Figure 1: Plot of $xy = 1$
The $x$-axis, that is the line $y = 0$, is the lower bound of the function $y = \dfrac{1}{x}$ for $x > 0$
Similarly, the $y$-axis, that is the line $x = 0$ is the left side bound of the function for $x \gt 0$.
There are three types of asymptotes. We will understand these asymptotes and see their examples in the following sections.
-----------book page break-----------
II. Horizontal Asymptotes
If the limit $\lim\limits_{x \rightarrow +\infty} f(x) = a$, exists, that is, the limit is finite, the $y = a$ is called the horizontal asymptote of $y = f(x)$.
Similarly, if the limit $\lim\limits_{x \rightarrow -\infty} f(x) = b$, exists then $y = b$ is a horizontal asymptote of $f(x)$.
Each of these two types of asymptotes is either the upper bound or the lower bound of the function $f(x)$.
Observe that the horizontal asymptote can intersect the function graph at one or more points. For example:
the curve $y = \dfrac{\sin x}{x}$ intersects the $x$-axis ($y = 0$) at multiple points, however the overall value of the curve tends to $0$ as $x \rightarrow \infty$ as shown in the following figure:

Therefore, the line $y = 0$ is an asymptote to the function $\dfrac{\sin x}{x}$.
-----------book page break-----------
III. Vertical Asymptotes
For any function $f(x)$ if the limit $\lim\limits_{x \rightarrow a} f(x)$ is $+\infty$ or $-\infty$ then the line $x = a$ is the vertical asymptote of $y = f(x)$.
Unlike horizontal asymptote, the vertical asymptote cannot intersect the function curve. It is easy to see why.
If there was a function, $f(x)$, which oscillates around its vertical asymptotes, intersecting it once or more, then, it implies that there will be some value/s of $x$ for which the function will have multiple values of $f(x)$, as shown in the following figure.
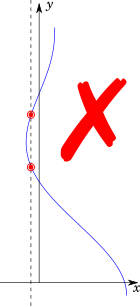
As per definition, this is not possible for a valid function.
-----------book page break-----------
IV. Slant (Oblique) Asymptotes
For any given function $y = f(x)$, if
$\lim\limits_{x \rightarrow +\infty} \dfrac{f(x)}{x} = k_1$ and $\lim\limits_{x \rightarrow +\infty} [f(x) - k_1x] = b_1$ exist, then,
$y = k_1x + b_1$ is an inclined right-side asymptote of $y = f(x)$
Similarly, if
$\lim\limits_{x \rightarrow -\infty} \dfrac{f(x)}{x} = k_2$ and $\lim\limits_{x \rightarrow -\infty} [f(x) - k_2x] = b_2$ exist, then,
$y = k_2x + b_2$ is an inclined left-side asymptote of $y = f(x)$.
V. Asymptotes Of Rational Functions
Rational functions are functions that can be represented as the ratio of two polynomials, as follows:
$f(x) = \dfrac{P(x)}{Q(x)}$ where $P(x)$ and $Q(x)$ are polynomials and $Q(x) \ne 0$.
For these types of rational functions, we will see some simple rules for finding the horizontal, vertical and slant asymptotes and will try to correlate these with the more generic rules using limits that we saw in the previous sections.
Rules For Horizontal Asymptote
If we have a rational function such that the degree of the denominator is greater than the degree of the numerator, then it is obvious that as $x$ grows larger, the magnitude of the denominator grows faster than the numerator. In this case as $x \rightarrow \infty$, the value of $f(x) \rightarrow \pm 0$. Let us take an example of this case and see it using both limits and this rule as well as concepts of limit.
-----------book page break-----------
Let:
$f(x) = \dfrac{x + 1}{x^3 - 3}$.
It is intuitive to see that $x^2 - 3$ grows at a much faster rate as compared to $x + 1$ with $x$. Hence $f(x) \rightarrow 0$ as $x \rightarrow \infty$.
Let us look at the solution by formally finding the limit:
$\lim \limits_{x \rightarrow \infty} \dfrac{x + 1}{x^3 - 3}$
Substituting $z = \dfrac{1}{x}$, we get the above limit as:
$\lim \limits_{z \rightarrow 0} \dfrac{\frac{1}{z} + 1}{\dfrac{1}{z^3} - 3}$ $\because$ as $x \rightarrow \infty$, $z \rightarrow 0$
$= \lim \limits_{z \rightarrow 0} \dfrac{z^2 + z^3}{1 - 3z^3} = \dfrac{0}{1} = 0$
In the above case, if $f(x)$ is of the form, $f(x) = \dfrac{P(x)}{Q(x)} + k$, where $k$ is a constant, then the horizontal asymptote is:
$y = k$
If the degree of the numerator and the degree of the denominator are the same, then the asymptote of that function can be found by dividing the coefficient of the highest degree term of the numerator by the coefficient of the highest degree term of the denominator and equating it to $y$.
Let us look at the following example.
-----------book page break-----------
Let:
$f(x) = \dfrac{3x^2 - 7x + 13}{5x^2 + 2x - 11}$
The degree of both the numerator and the denominator functions, is $2$.
Applying the above rule, and dividing the coefficients of the both $x^2$ terms, we get the asymptote as $y = \dfrac{3}{5}$
Using limit as $x \rightarrow \infty$, we get:
$\lim \limits_{x \rightarrow \infty} \dfrac{3x^2 - 7x + 13}{5x^2 + 2x - 11}$
Substituting $z = \dfrac{1}{x}$, we get, the above limit as:
$\lim \limits_{z \rightarrow 0} \dfrac{\frac{3}{z^2} - \frac{7}{z} + 13}{\frac{5}{z^2} + \frac{2}{z} - 11}$
$= \lim \limits_{z \rightarrow 0} \dfrac{3 - 7z + 13z^2}{5 + 2z - 11z^2} = \dfrac{3}{5}$
Now we can easily see that when the degrees of the numerator and the denominator are the same, and $x$ tends to $\infty$, only the coefficients of the the most significant terms remain, the other terms become insignificant, since their growth rate is much smaller than the highest degree terms.
Note that if the degree of the numerator is greater than that of the denominator, it will be an ever increasing or decreasing function, and will not tend to a specific value, and hence, will not have a horizontal asymptote.
-----------book page break-----------
Rule For Vertical Asymptote
For any rational function, $f(x) = \dfrac{P(x)}{Q(x)}$, if $Q(x)$ is of order $n$, then, $Q(x)$ has $n$ zeros (real or imaginary). If it has $k$ real roots at $x_1, x_2,... x_k$, such that $x = x_i$ is not a zero of $P(x)$, then each of the lines $x = x_i$ is a vertical asymptote of $f(x)$.
It is easy to see this rule, because for each real root $x = x_i$,
$\lim \limits_{x \rightarrow x_i} Q(x) = 0$, but $P(x_i) \ne 0$
Therefore, $\lim \limits_{x \rightarrow x_i} \dfrac{P(x)}{Q(x)} = \infty$ and hence, gives us a vertical asymptote.
Rule For Oblique Asymptote
For any rational function $f(x) = \dfrac{P(x)}{Q(x)}$, if the order of $P(x)$ exceeds that of $Q(x)$ by exactly $1$, then, $f(x)$ has an oblique asymptote.
Observe that if $Q(x)$ is of order $n$ and $P(x)$ is of order $n + 1$, then dividing $P(x)$ by $Q(x)$ will give a quotient $q(x)$ of order $1$, and $y = q(x)$ will be a straight line, which will be an asymptote to $f(x)$.
Let us consider the following example.
Let:
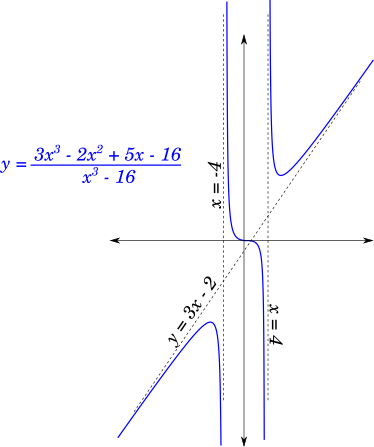
$f(x) = \dfrac{P(x)}{Q(x)} = \dfrac{3x^3 - 2x^2 + 5x - 16}{x^2 - 16}$
Dividing $P(x)$ by $Q(x)$ using the long division method, we get the quotient as $3x - 2$ and the remainder as $53x - 48$. Since $3x - 2$ is the quotient,
$y = 3x - 2$ is line which has a finite, non-zero slope, it is a slant asymptote of $f(x)$.
Since the denominator has two real roots at $x = \pm 4$, the function f(x) also has two vertical asymptotes $x = 4$ and $x = -4$.
-----------book page break-----------
Now we will solve the same problem using limits and see what we get for the oblique asymptote.
$\lim \limits_{x \rightarrow \infty} \dfrac{f(x)}{x}$
$= \lim \limits_{x \rightarrow \infty} \dfrac{3x^3 - 2x^2 + 5x - 16}{(x^2 - 16)x}$
$= \lim \limits_{x \rightarrow \infty} \dfrac{3x^3 - 2x^2 + 5x - 16}{x^3 - 16x}$
Substituting $x = \dfrac{1}{z}$ we get the limit as:
$= \lim \limits_{z \rightarrow 0} \dfrac{\frac{3}{z^3} - \frac{2}{z^2} + \frac{5}{z} - 16}{\frac{1}{z^3} - \frac{16}{z}}$
$= \lim \limits_{z \rightarrow 0} \dfrac{3 - 2z + 5z^2 - 16z^3}{1 - 16z^2}$
$= 3$
Now, for the second limit:
$\lim \limits_{x \rightarrow \infty} [f(x) - 3x]$
$\lim \limits_{x \rightarrow \infty} [f(x) - 3x]$
$= \lim \limits_{x \rightarrow \infty} \left[\dfrac{3x^3 - 2x^2 + 5x - 16}{x^2 - 16} - 3x \right]$
-----------book page break-----------
$= \lim \limits_{x \rightarrow \infty} \dfrac{(3x^3 - 2x^2 + 5x - 16) - (3x^3 - 16x)}{x^2 - 16}$
$= \lim \limits_{x \rightarrow \infty} \dfrac{- 2x^2 + 21x - 16}{x^2 - 16}$
Substituting $x = \dfrac{1}{z}$, we get the limit as:
$\lim \limits_{z \rightarrow 0} \dfrac{- \dfrac{2}{z^2} + \dfrac{21}{z} - 16}{\dfrac{1}{z^2} - 16}$
$\lim \limits_{z \rightarrow 0} \dfrac{- 2 + 21z - 16z^2}{1 - 16z^2}$
$= -2$
Therefore,
$y = 3x - 2$ is a right-side asymptote of $f(x)$
Similarly, taking the limits as $x \rightarrow -\infty$, we will see that $y = 3x - 2$ is also a left-side asymptote of $f(x)$.
Also, observe that there are two vertical asymptotes at $x = \pm 4$, since the denominator $Q(x) = x^2 - 16$ has two real roots at $x = \pm 4$
-----------book page break-----------
Now let us look at the following figure showing the plot of the given function and the asymptotes.
Observe that the line $y = 3x - 2$ is a left-side asymptote of the curve of $f(x)$ for the upper portion of the curve, and it is the right-side asymptote for the lower portion of the curve.
-----------book page break-----------
VI. Asymptotes Of Irrational Functions
In the previous section we saw some rules which can be applied to find the asymptotes of rational functions, without using limits. However for irrational functions we do need to use limits to find the asymptotes. In this section, we will use the concepts from Section IV to derive the equation of the asymptotes of a standard hyperbola of the form:
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$
Rearranging the equation to express $y$ as a function of $x$, we get:
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$
$\Rightarrow \dfrac{y^2}{b^2} = \dfrac{x^2}{a^2} - 1$
$\Rightarrow y^2 = \dfrac{b^2x^2}{a^2} - b^2$
$y = \pm \sqrt{\dfrac{b^2x^2}{a^2} - b^2}$
Taking the first function as $f(x) = \sqrt{\dfrac{b^2x^2}{a^2} - b^2}$ and taking the limit of $\dfrac{f(x)}{x}$ as $x \rightarrow \infty$, we get:
$\lim \limits_{x \rightarrow \infty} \dfrac{\sqrt{\dfrac{b^2x^2}{a^2} - b^2}}{x}$
-----------book page break-----------
$= \lim \limits_{x \rightarrow \infty} \sqrt{\dfrac{b^2}{a^2} - \dfrac{b^2}{x^2}}$ (as $x \rightarrow \infty$, $\dfrac{b^2}{x^2} \rightarrow 0$)
$= \lim \limits_{x \rightarrow \infty} \sqrt{\dfrac{b^2}{a^2}}$
$= \dfrac{b}{a}$
Now we need to find the limit of $\sqrt{\dfrac{b^2x^2}{a^2} - b^2} - \dfrac{bx}{a}$ as $x \rightarrow \infty$
$\lim \limits_{x \rightarrow \infty} \sqrt{\dfrac{b^2x^2}{a^2} - b^2} - \dfrac{bx}{a}$
$= \lim \limits_{x \rightarrow \infty} \sqrt{\dfrac{b^2x^2 - b^2a^2}{a^2}} - \dfrac{bx}{a}$
$= \lim \limits_{x \rightarrow \infty} \dfrac{b}{a} \left(\sqrt{x^2 - a^2} - \sqrt{x^2} \right)$
$= \dfrac{b}{a} \lim \limits_{x \rightarrow \infty} x\left(\sqrt{1 - \dfrac{a^2}{x^2}} - 1 \right)$
$= \dfrac{b}{a} \lim \limits_{z \rightarrow 0} \dfrac{\sqrt{1 - a^2z^2} -1}{z} $
We can see above that the as $z \rightarrow 0$, the above limit tends to the indeterminate form $\dfrac{0}{0}$, therefore, using L'Hospital's rule we get:
-----------book page break-----------
$\dfrac{b}{a} \lim \limits_{z \rightarrow 0} \dfrac{\sqrt{1 - a^2z^2} -1}{z}$
$= \dfrac{b}{a} \lim \limits_{z \rightarrow 0} \dfrac{\dfrac{d}{dz}(\sqrt{1 - a^2z^2} -1)}{\dfrac{d}{dz}(z)}$
$= \dfrac{b}{a} \lim \limits_{z \rightarrow 0} \dfrac{\frac{1}{2}(1 - a^2z^2)^{-\frac{1}{2}}(-2a^2z)}{1}$
$= \dfrac{b}{a} \lim \limits_{z \rightarrow 0} \dfrac{-2a^2z}{2\sqrt{1 - a^2z^2}}$
$= \dfrac{b}{a} \cdot \dfrac{0}{1} = 0$
Therefore, we get $y = \dfrac{bx}{a}$ as one of the asymptotes.
Similarly, using the second function $y = f(x) = -\sqrt{\dfrac{b^2x^2}{a^2} - b^2}$, we will get $y = -\dfrac{bx}{a}$ as another asymptote.
Therefore, the two asymptotes of the standard hyperbola are $y = \pm \dfrac{bx}{a}$