The Unit Circle & Trigonometric Ratios
We learnt about trigonometric ratios of common angles in the first quadrant , where all the trigonometric ratios are positive. In this part we will learn about ratios in the other quadrants.
I. The Unit Circle
The following widget shows a circle of radius $1$ unit and the origin $(0, 0)$ as the center. This is called the unit circle. In this chapter we will see how various trigonometric ratios are related to the unit circle.
Try rotating point $P$ (the red dot) along the circle, and see how the values of the trigonometric ratios behave in all the four different quadrants. You can rotate the point in clockwise or counter-clockwise direction to see the ratios of negative or positive angles.
-----------book page break-----------
Points $A$ and $B$ are the feet of the perpendiculars drawn from $P$ to the $x$ and $y$ axes respectively. A tangent $TT'$ to the unit circle is drawn at $P$. Let this tangent intersect the $x$ and $y$ axes at $T$ and $T'$ respectively.
In $\triangle APO$,
$\angle POA = \theta$ and $\angle PAO = 90^\circ$
Let the coordinates of $P$ and any time be $(x, y)$
Let us consider $\triangle OPA$.
$OP = 1$
$OA = x$
$OB = y$
The above relations are valid no matter which quadrant the point $P$ lies or if angle $\theta$ is positive or negative.
Now, we can see that for a unit circle centered at the origin, the coordinates of a point $P$ on the circumference, directly gives us the ratios of the angle formed by that point with the centre and the positive $X$ axis. This will be valid for all points on the circumference of the unit circle, no matter which quadrant the point is in.
Considering $\triangle PTO$, $\angle TOP = \theta$, $\angle OPT = 90^\circ$, $OP = r = 1$
Therefore, $\tan \theta = \dfrac{PT}{OP} = PT$
Similarly, using $\triangle PT'O$, we can show that $\angle PT'O = \theta$
and $\cot \theta = T'P$
-----------book page break-----------
II. Angles In The First Quadrant
Let us take any point $P$ on the circumference of the unit circle in the first quadrant and draw the line $OP$. Let us call the angle that $OP$ makes with the positive $X$ axis as $\theta$. We drop a perpendicular from point $P$ on the $X$ axis at $A$ and on the $Y$ axis at $B$, as shown in the figure below:
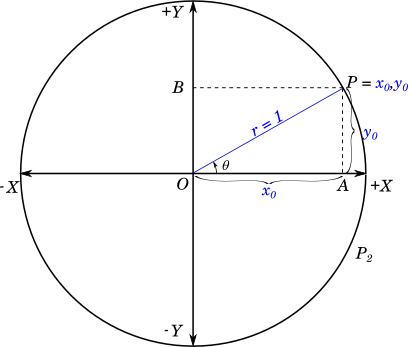
We have $AP = OB = y_0$ and $OA = BP = x_0$.
-----------book page break-----------
The trigonometric ratios for angle $\theta$ will be as follows:
$sin(\theta) = \dfrac{AP}{OP} = \dfrac{y_0}{r} = \dfrac{y_0}{1} = y_0$ $eqn\ \ \ ...\ (i)$
$cos(\theta) = \dfrac{OA}{OP} = \dfrac{x_0}{r} = \dfrac{x_0}{1} = x_0$ $eqn\ \ \ ...\ (ii)$
$tan(\theta) = \dfrac{AP}{OA} = \dfrac{y_0}{x_0}$ $eqn\ \ \ ...\ (iii)$
Now let us find the ratios of angles of the form $(90 - \theta)$.
For this we will rotate the radius $OP$ to coincide with the positive $Y$ axis, and rotate it back in the clockwise direction by an angle $\theta$, to the point $P^\prime$, as shown in the following figure:
-----------book page break-----------
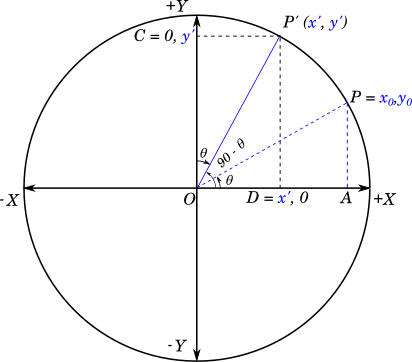
The resulting $\angle P^\prime OX$ will be equal to $(90 - \theta)$.
Considering $\triangle POA$ and $\triangle P^\prime OC$
$OP = OP^\prime$ (radii of the same circle)
$\angle POA = \angle P^\prime OC$ (both are equal to $\theta$)
$\angle PAO = \angle P^\prime CO$ (both are $90^\circ$)
$\therefore \triangle POA \cong \triangle P^\prime OC$
$\therefore y^\prime = DP^\prime = OC = OA = x_0$
$\therefore sin(90 - \theta) = x_0$
-----------book page break-----------
We know from $(ii)$ that $x_0 = cos(\theta)$
$\therefore sin(90 - \theta) = cos(\theta)$
Similarly,
$x^\prime = CP^\prime = OD = AP = y_0$
$\Rightarrow cos(90 - \theta) = x^\prime = y_0$
We know from $(i)$ that $y_0 = sin(\theta)$
$\therefore cos(90 - \theta) = sin(\theta)$
And,
$tan(90 - \theta) = \dfrac{y^\prime}{x^\prime} = \dfrac{x_0}{y_0} = \dfrac{1}{\frac{y_0}{x_0}} = \dfrac{1}{tan(\theta)}$.
We know from our inverse relationship from , that $\dfrac{1}{tan(\theta)} = cot(\theta)$
$\therefore tan(90 - \theta) = cot(\theta)$
That is how the name of these ratios have evolved. As you might have observed that each ratio for an angle $\theta$ is same as the complementary ratio for $(90 - \theta)$
Like $sine(90 - \theta) = cosine(\theta)$ and $cosine(90 - \theta) = sine(\theta)$
$secant(90 - \theta) = cosecant(\theta)$ and $cosecant(90 - \theta) = secant(\theta)$
$tangent(90 - \theta) = cotangent(\theta)$ and $cotangent(90 - \theta) = tangent(\theta)$
The ratios prefixed with the $\unicode{0x201C}co\unicode{0x201D}$ prefix mean the complementary ratio.
Observe that points $P$ and $P^\prime$ are in the first quadrant, $x_0$, $y_0$, $x^\prime$ and $y^\prime$ are positive, and $r$ being the radius of a circle, is always positive, hence all the ratios listed above and their inverses are also positive.
-----------book page break-----------
III. Angles In The Second Quadrant
Now let us take the line $OP$ from the figure in the previous section, and rotate it around point $O$ counter-clockwise by $90^\circ$, and call this new point on the circumference as $P_1$ at $x_1, y_1$. Since this angle is greater than $90^\circ$ and $\theta$ is acute, $P_1$ will be in the second quadrant. In the second quadrant $x$ values are negative and $y$ values are positive.
From here on, we will mark all the negative values in red, and the positive values in blue.
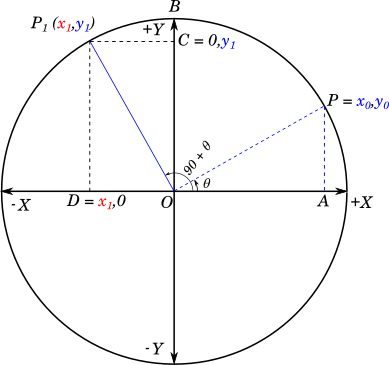
-----------book page break-----------
In the previous figure, $\triangle OPA \cong \triangle OP_1C$
(We will leave this as an exercise for you. Use the $AAS$ rule to prove congruence of these two triangles)
We have $\textcolor{red}{x_1} = -\textcolor{blue}{y_0}$
and $\textcolor{blue}{y_1} = \textcolor{blue}{x_0}$
$sin(90 + \theta) = \textcolor{blue}{y_1} = \textcolor{blue}{x_0}$
$cos(90 + \theta) = \textcolor{red}{x_1} = -\textcolor{blue}{y_0}$
$tan(90 + \theta) = \dfrac{\textcolor{blue}{y_1}}{\textcolor{red}{x_1}} = -\dfrac{\textcolor{blue}{x_0}}{\textcolor{blue}{y_0}} = -\dfrac{1}{\frac{\textcolor{blue}{y_0}}{\textcolor{blue}{x_0}}}$
From equations $(i)$, $(ii)$ and $(iii)$ of $Section\ I$, we have:
$\textcolor{blue}{x_0} = cos(\theta)$
$\textcolor{blue}{y_0} = sin(\theta)$
$\dfrac{\textcolor{blue}{y_0}}{\textcolor{blue}{x_0}} = tan(\theta)$
Therefore, we have:
$sin(90 + \theta) = cos(\theta)$
$cos(90 + \theta) = -sin(\theta)$
$tan(90 + \theta) = -\dfrac{1}{tan(\theta)} = -cot(\theta)$
Now, let us look at the trigonometric ratios of angles of the form $(180 - \theta)$.
-----------book page break-----------
For, this we will take our original unit circle from $Section\ I$, take the radius $OP$ and rotate it to make it concurrent with the negative $X$ axis, then rotate it back in the clockwise direction by an angle of $\theta$. The value of $\angle XOP_2$ will be $(180 - \theta)$.
Since $\theta$ is acute, $\angle XOP_2$ will be in the second quadrant, as shown in the figure below:
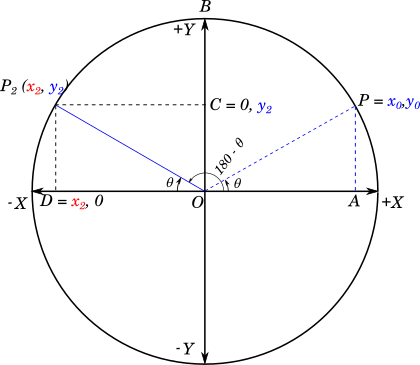
$\triangle POA \cong \triangle P_2OD$, therefore we have:
-----------book page break-----------
$\textcolor{blue}{y_2} = \textcolor{blue}{y_0}$
$\textcolor{red}{x_2} = -\textcolor{blue}{x_0}$
$sin(180 - \theta) = \textcolor{blue}{y_2} = \textcolor{blue}{y_0} = sin(\theta)$
$cos(180 - \theta) = \textcolor{red}{x_2} = -\textcolor{blue}{x_0} = -cos(\theta)$
$tan(180 - \theta) = \dfrac{\textcolor{blue}{y_2}}{\textcolor{red}{x_2}} = -\dfrac{\textcolor{blue}{y_0}}{\textcolor{blue}{x_0}} = -tan(\theta)$
Now that we have the main $3$ ratios for both $(90 + \theta)$ and $(180 - \theta)$, we can find the inverses of these ratios:
$cosec(90 + \theta) = \dfrac{1}{sin(90 + \theta)} = \dfrac{1}{cos(\theta)} = sec(\theta)$
$sec(90 + \theta) = \dfrac{1}{cos(90 + \theta)} = \dfrac{1}{-sin(\theta)} = -cosec(\theta)$
$cot(90 + \theta) = \dfrac{1}{tan(90 + \theta)} = \dfrac{1}{-cot(\theta)} = -tan(\theta)$
Similarly,
$cosec(180 - \theta) = \dfrac{1}{sin(180 - \theta)} = \dfrac{1}{sin(\theta)} = cosec(\theta)$
$sec(180 - \theta) = \dfrac{1}{cos(180 - \theta)} = \dfrac{1}{-cos(\theta)} = -sec(\theta)$
$cot(180 - \theta) = \dfrac{1}{tan(180 - \theta)} = \dfrac{1}{-tan(\theta)} = -cot(\theta)$
We also need to observe that in the second quadrant only $sin$ and its inverse $cosec$ are positive, remaining all ratios are negative.
-----------book page break-----------
IV. Angles In The Third Quadrant
To get the corresponding ratios in the third quadrant we can take the radius $OP$ from our diagram in $Section\ I$, and rotate it counter-clockwise by $180^\circ$ and get the new radius $OP_3$.
$\angle P_3OX = 180 + \theta$ and since $\theta$ is acute, this angle is in the third quadrant, and therefore both $x$ and $y$ coordinates of $P_3$ will be negative. Like before, we can drop the perpendiculars from $P_3$ to the $X$ and $Y$ axes at point $D$ and $C$ respectively as shown in the figure below:
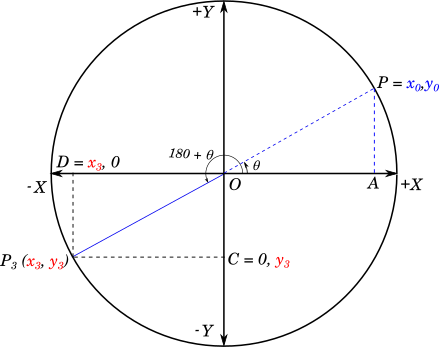
$\triangle P_3OD \cong \triangle POA$
-----------book page break-----------
$\textcolor{red}{y_3} = -\textcolor{blue}{y_0}$
$\textcolor{red}{x_3} = -\textcolor{blue}{x_0}$
We have the following values for our main trigonometric ratios:
$sin(180 + \theta) = \textcolor{red}{y_3} = -\textcolor{blue}{y_0} = -sin(\theta)$
$cos(180 + \theta) = \textcolor{red}{x_3} = -\textcolor{blue}{x_0} = -cos(\theta)$
$tan(180 + \theta) = \dfrac{\textcolor{red}{y_3}}{\textcolor{red}{x_3}} = \dfrac{-\textcolor{blue}{y_0}}{-\textcolor{blue}{x_0}} = \dfrac{\textcolor{blue}{y_0}}{\textcolor{blue}{x_0}} = tan(\theta)$
Now, let us look at the main ratios for angles of the form $(270 - \theta)$
For this we can rotate the radius $OP$ to coincide with the negative $Y$ axis, and then rotate it back in the clockwise direction by an angle of $\theta$. In the following figure, $P_4OX = 270 - \theta$
-----------book page break-----------
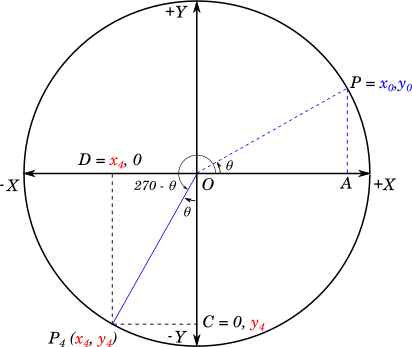
$\triangle P_4OC \cong \triangle POA$ with
$\textcolor{red}{y_4} = -\textcolor{blue}{x_0}$
$\textcolor{red}{x_4} = -\textcolor{blue}{y_0}$
We have the following values for our main trigonometric ratios:
$sin(270 - \theta) = \textcolor{red}{y_4} = -\textcolor{blue}{x_0} = -cos(\theta)$
$cos(270 - \theta) = \textcolor{red}{x_4} = -\textcolor{blue}{y_0} = -sin(\theta)$
-----------book page break-----------
$\tan(270 - \theta) = \dfrac{\textcolor{red}{y_4}}{\textcolor{red}{x_4}} = \dfrac{-\textcolor{blue}{x_0}}{-\textcolor{blue}{y_0}} = \dfrac{\textcolor{blue}{x_0}}{\textcolor{blue}{y_0}} = \dfrac{1}{\dfrac{\textcolor{blue}{y_0}}{\textcolor{blue}{x_0}}} = \dfrac{1}{tan(\theta)} = cot(\theta)$
-----------book page break-----------
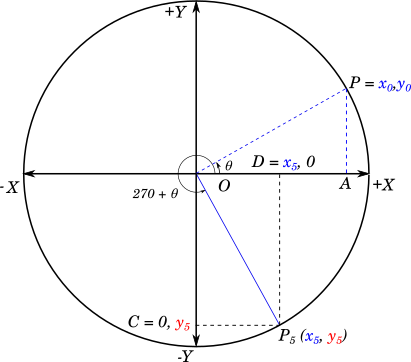
V. Angles In The Fourth Quadrant
To find the ratios of an angle in the fourth quadrant, we can take the line $OP$ is rotate it about $O$ by $270^\circ$. The resulting angle, $\angle P_5OX$, will be $270 + \theta$, and will be in the fourth quadrant.
We will draw perpendiculars from $P$, $P_5$, to both axes, as before, and mark them appropriately.
-----------book page break-----------
$\triangle P_5OC \cong \triangle POA$, therefore we have:
$\textcolor{blue}{x_5} = \textcolor{blue}{y_0}$
$\textcolor{red}{y_5} = -\textcolor{blue}{x_0}$
$sin(270 + \theta) = \textcolor{red}{y_5} = -\textcolor{blue}{x_0} = -cos(\theta)$
$cos(270 + \theta) = \textcolor{blue}{x_5} = \textcolor{blue}{y_0} = sin(\theta)$
$tan(270 + \theta) = \dfrac{\textcolor{red}{y_5}}{\textcolor{blue}{x_5}} = \dfrac{-\textcolor{blue}{x_0}}{\textcolor{blue}{y_0}} = -\dfrac{1}{\frac{\textcolor{blue}{y_0}}{\textcolor{blue}{x_0}}} = -\dfrac{1}{tan(\theta)} = -cot(\theta)$
Now, let us look at the angles of the form $(360 - \theta)$.
For this we can rotate the radius $OP$ such that it coincides with the positive $X$ axis and then rotate it back clockwise by an angle of $\theta$.
Observe, that this is also the same as taking a $0^\circ$ angle, and rotate the radius in the negative direction by an angle $\theta$, which gives us $-\theta$. Therefore, all the ratios that we will compute for $(360 - \theta)$ will also be valid for $-\theta$
-----------book page break-----------
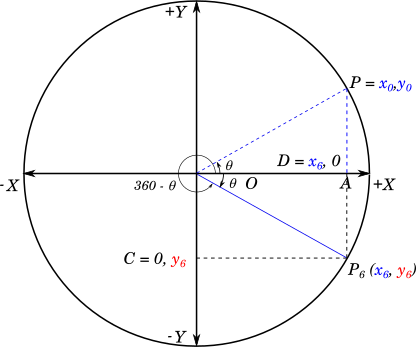
$\triangle P_6OD \cong \triangle POD$
$\textcolor{blue}{x_6} = \textcolor{blue}{x_0}$
$\textcolor{red}{y_6} = -\textcolor{blue}{y_0}$
$sin(360 - \theta) = sin(-\theta) = \textcolor{red}{y_6} = -\textcolor{blue}{y_0} = -sin(\theta)$
$cos(360 - \theta) = cos(-\theta) = \textcolor{blue}{x_6} = \textcolor{blue}{x_0} = cos(\theta)$
$tan(360 - \theta) = tan(-\theta) = \dfrac{\textcolor{red}{y_6}}{\textcolor{blue}{x_6}} = \dfrac{-\textcolor{blue}{y_0}}{\textcolor{blue}{x_0}} = -\dfrac{\textcolor{blue}{y_0}}{\textcolor{blue}{x_0}} = -tan(\theta)$
-----------book page break-----------
VI. Summary
Now let us summarise the results we derived so far, in a tabular form. For any angle $\theta$
| $1st\ Quadrant$ | $2nd\ Quadrant$ | $3rd\ Quadrant$ | $4th\ Quadrant$ | |||||
| $\theta$ | $(90 - \theta)$ | $(90 + \theta)$ | $(180 - \theta)$ | $(180 + \theta)$ | $(270 - \theta)$ | $(270 + \theta)$ | $(360 - \theta)$ | |
| $sine$ | $sin(\theta)$ | $cos(\theta)$ | $cos(\theta)$ | $sin(\theta)$ | $-sin(\theta)$ | $-cos(\theta)$ | $-cos(\theta)$ | $-sin(\theta)$ |
| $cosecant$ | $cosec(\theta)$ | $sec(\theta)$ | $sec(\theta)$ | $cosec(\theta)$ | $-cosec(\theta)$ | $-sec(\theta)$ | $-sec(\theta)$ | $-cosec(\theta)$ |
| $cosine$ | $cos(\theta)$ | $sin(\theta)$ | $-sin(\theta)$ | $-cos(\theta)$ | $-cos(\theta)$ | $-sin(\theta)$ | $sin(\theta)$ | $cos(\theta)$ |
| $secant$ | $sec(\theta)$ | $cosec(\theta)$ | $-cosec(\theta)$ | $-sec(\theta)$ | $-sec(\theta)$ | $-cosec(\theta)$ | $cosec(\theta)$ | $sec(\theta)$ |
| $tangent$ | $tan(\theta)$ | $cot(\theta)$ | $-cot(\theta)$ | $-tan(\theta)$ | $tan(\theta)$ | $cot(\theta)$ | $-cot(\theta)$ | $-tan(\theta)$ |
| $cotangent$ | $cot(\theta)$ | $tan(\theta)$ | $-tan(\theta)$ | $-cot(\theta)$ | $cot(\theta)$ | $tan(\theta)$ | $-tan(\theta)$ | $-cot(\theta)$ |
To read the above table you can pick any ratio from the first column and any angle in any quadrant from the first row. The corresponding cell value will give the corresponding ratio. For example,
$secant(270 - \theta) = -cosine(\theta)$.
Also, observe that, although we have derived all the relationships in the previous sections assuming $\theta$ to be positive and acute, however these relationships hold for any value of $\theta$.
-----------book page break-----------
Now let us look at how we can easily remember the signs of the various ratios in different quadrants. In the first quadrant everything is positive, in the second quadrant $sine$ and its inverse $cosec$ are positive, remaining all are negative. In the third quadrant $tan$ and its inverse $cot$ are positive, rest all are negative, and in the fourth quadrant $cos$ and its inverse $sec$ are positive, rest all are negative.
Hence, if you just remember the following sequence $All\ Sin\ Tan\ Cos$, that is good enough, and you must know that when a number is positive, its inverse is also positive.
That gives us our first rule.
Rule 1: Signs Of Ratios
$all,\ sin,\ tan,\ cos$
Starting with the first quadrant, this is the list of positive ratios, and of course, their inverses.
Next, let us look at how to remember for which cases a ratio switches to and from its complementary ratio, that is, when $sin$ becomes $cos$ or for which cases $sin$ remains $sin$.
For any angle of the form $180 \pm \theta$ or $360 \pm \theta$ the ratio magnitude remains the same, only the sign may or may not change, depending on which quadrant it is in.
For example $sin(180 - \theta)$ remains $sin(\theta)$, $tan(180 + \theta)$ remains as $tan(\theta)$, $cos(360 - \theta)$ remain $cos(\theta)$, etc.
While for angles of the form $(90 \pm \theta)$ or $(270 \pm \theta)$ all the ratio change to their corresponding $complementary$ ratios, with a corresponding sign change:
For example $sin(90 - \theta) = cos(\theta)$, ($cos$ is the complementary ratio of $sin$),
Similarly $cosec(90 + \theta)$ becomes its complementary ratio $sec(\theta)$.
Same with the case of $(270 \pm \theta)$, where each ratio changes to its complementary ratio.
-----------book page break-----------
So we will divide all the possibilities into just two categories, which are, odd multiples of $90$ and even multiples of $90$, and remember how the ratios of the form $(90m \pm \theta)$ change.
Rule 2:
And our simple rule to remember is that:
If $m$ is even, then all the ratios for $(90m \pm \theta)$ has the same magnitude as that of the same ratio of $\theta$.
If $m$ is odd, then all the ratios for $(90m \pm \theta)$ has the same magnitude as that of the corresponding complementary ratio of $\theta$.