Diagonal And Sides Of Parallelogram

Theory

The sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of the four sides.

That is, for any given parallelogram, $ABCD$,

$AC^2 + BD^2 = AB^2 + BC^2 + CD^2 + DA^2$

or equivalently, since opposite sides of a parallelogram are equal,

$AC^2 + BD^2 = 2AB^2 + 2BC^2$

Construction

We draw a parallelogram $ABCD$ as shown below, and drop perpendiculars from to vertices $C$ and $D$ the opposite sides at points $E$ and $F$.

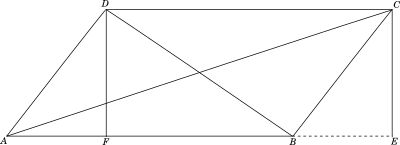
Proof

Considering right-angled $\triangle CEA$,

$AC^2 = AE^2 + CE^2$

$\Rightarrow AC^2 = (AB + BE)^2 + CE^2$

$\Rightarrow$ $AC^2 = AB^2 + BE^2 + 2AB.BE + CE^2$ $...eqn(i)$

-----------book page break-----------

Similarly, considering right-angled $\triangle DFB$,

$DB^2 = BF^2 + DF^2$

$\Rightarrow DB^2 = (AB - AF)^2 + DF^2$

$\Rightarrow$ $DB^2 = AB^2 + AF^2 - 2AB.AF + DF^2$ $...eqn(ii)$

Considering $\triangle s\ DAF$ and $CBE$

$\angle DAF = \angle CBE$

$\angle DFA = \angle CEB$

$AD = BC$

$\therefore \triangle DAF \cong \triangle CBE$

$\therefore AF = BE$

Adding $eqn\ (i)$ and $eqn\ (ii)$,

$AC^2 + DB^2 = AB^2 + BE^2 + 2AB.BE + CE^2 + AB^2 + AF^2$

$- 2AB.AF + DF^2$

$\Rightarrow AC^2 + DB^2 = AB^2 + BE^2 + 2AB.AF + CE^2 + AB^2 + AF^2$

$- 2AB.AF + DF^2$

$\Rightarrow AC^2 + DB^2 = AB^2 + BE^2 + CE^2 + AB^2 + AF^2 + DF^2$

Since $\triangle s$ $AFD$ and $BEC$ are right-angled,

$AF^2 + DF^2 = AD^2$ and $BE^2 + CE^2 = BC^2$

$\therefore AC^2 + DB^2 = AB^2 + BC^2 + AB^2 + AD^2$

$\Rightarrow AC^2 + DB^2 = AB^2 + BC^2 + CD^2 + DA^2$

or substituting $CD = AB$ and $DA = AB$,

$AC^2 + DB^2 = 2AB^2 + 2BC^2$