Basic Definitions In Geometry - Points, Lines & Plane
I. Points
A point is a specific location. In geometry point is denoted by a small dot $(\bullet)$. But that is only to indicate the location of a point. A real point does not have any length or breadth.
Points are often identified by a letter from the alphabet written next to the point. The diagram below shows three such points name $A,\ B$ and $C$ respectively.

II. Lines
Try this out at. Take a sharpened pencil, and place the tip on a piece of a paper and drag the pencil in whichever direction you want to. The mark left on the the point is the path that your pencil took on the paper. This is a line.
In reality a line has only length and no width.
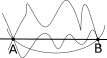
Now let us mark two points $A$ and $B$ on that paper, and try to draw a few lines which pass through those two points.
As you can see in the below diagram, it is possible to draw many different lines through two points.
-----------book page break-----------
The shortest possible line through these two points is a
$\underline{straight\ line}$
.
As you can easily see the a line can be extended to any length on either side.
A straight line can be named by naming any two points on the line. A straight line that can be extended on either side is denoted by the name of the line and a $\leftrightarrow$ symbol on top of the name. The line in the above diagram is indicated using $\overset{\leftrightarrow}{AB}$
III. Rays
If a line is such, that it is fixed by a point at one end and is extended infinitely at the other end, it is called a $ray$, as shown in the diagram below.

This is indicated by the name of the line and a $\texttip{\Rightarrow}{follows that}$ symbol above it. The line shown above can be shown using $\overset{\rightarrow}{AB}$
Be careful about the direction of the ray and the name of the line. Unlike the above ray, the ray shown below should be shown as $\overset{\rightarrow}{BA}$
-----------book page break-----------
IV. Line Segment
When a line is fixed (terminated) on both ends by two points it is called a
line segment
, and is shown with a $-$ symbol above the name of the line. The line in the diagram below is shown using $\overline{AB}$
A line segment has a fixed length.
V. Planes
We saw earlier that a point can be moved around to get a line. Similarly, we can move around a line in various direction to obtain a surface. When we have a straight surface (like that of a mirror, the surface of a table) that can extend infinitely on any side, that is called a plane.
Now let us understand a few things about points, lines and planes.
$What\ do\ we\ get\ when\ two\ lines\ intersect\ each\ other?$ Answer:
We get a point
, as shown below.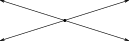
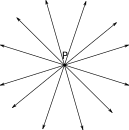
$How\ many\ lines\ can\ pass\ through\ any\ given\ single\ point?$ Answer:
Infinitely many
.-----------book page break-----------
As shown in the diagram, if you take a point $P$ and start drawing lines, each of them passing through this point, and each rotated by a very small angle, then you can draw a very large number of lines. As you draw lines at smaller and smaller angles you can draw infinitely many lines, all passing through the same point.
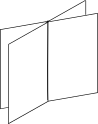
$What\ do\ we\ get\ when\ two\ planes\ intersect\ each\ other?$ Answer:
A line
, as shown below.You can imagine the walls, floor and ceiling of your room as planes and wherever two planes meet you can see a line.
$How\ many\ planes\ can\ pass\ through\ a\ line?$ Answer:
Infinite
.