Ceva's Theorem

$\underline{Theorem}:$

In a $\triangle ABC$ for any internal point $P$, if we extend $AP$, $BP$ and $CP$ to meet the opposite sides at $D$, $E$ and $F$ respectively, then

$\dfrac{AF\cdot BD \cdot CE}{FB \cdot DC \cdot EA} = 1$

$\underline{Construction}:$

We draw the diagram as described in the theory, no additional construction required.

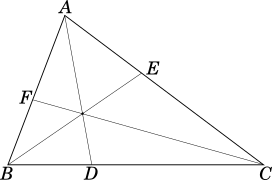
$\underline{Proof}:$

Considering $\triangle PAF$ and $\triangle PFB$, with $PF$ and $FB$ as their respective bases, then both triangles have equal height, and their areas are proportional to their bases.

$\therefore \dfrac{[PAF]}{[PFB]} = \dfrac{AF}{FB}$

-----------book page break-----------

Similarly considering $\triangle CAF$ and $\triangle CFB$

$\dfrac{[CAF]}{[CFB]} = \dfrac{AF}{FB}$

$\therefore \dfrac{AF}{FB} = \dfrac{[CAF]}{[CFB]} = \dfrac{[PAF]}{[PFB]} = k$

$\therefore \dfrac{[CAF]}{[CFB]} = k$

$\therefore [CAF] = k \times [CFB]$ $...eqn(i)$

and

$[PAF] = k \times [PFB]$ $...eqn(ii)$

$eqn(i) - eqn(ii)$ gives us:

$[CAF] - [PAF] = k ([CFB] - [PFB])$

$\Rightarrow [CPA] = k [CPB]$

$\therefore \dfrac{[CPA]}{[CPB]} = k = \dfrac{AF}{FB}$

$\Rightarrow$ $\dfrac{AF}{FB} = \dfrac{[CPA]}{[CPB]}$ $...eqn(iii)$

Similarly, we can show that:

$\dfrac{BD}{DC} = \dfrac{[APB]}{[APC]}$ $...eqn(iv)$ and

$\dfrac{CE}{EA} = \dfrac{[BPC]}{[BPA]}$ $...eqn(v)$

-----------book page break-----------

$eqn(iii)$ $\times$ $eqn(iv)$ $\times$ $eqn(v)$ gives us:

$\dfrac{AF}{FB} \times \dfrac{CE}{EA} \times \dfrac{CE}{EA}= \dfrac{[CPA]}{[CPB]} \times \dfrac{[APB]}{[APC]} \times \dfrac{[BPC]}{[BPA]}$

$\dfrac{AF\cdot BD \cdot CE}{FB \cdot DC \cdot EA} = 1$