Parallel Lines & Transversal
I. Introduction
We will learn a few things about parallel lines. Let us take any two lines $p$ and $q$, as shown in Figure-1 below:
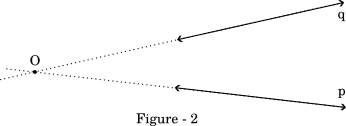
What happens if we extend the lines towards the left. They will meet each other at some point, as shown in the figure below. The point where these lines cross each other is called the the $point\ of\ intersection$, marked as $O$ in the diagram.
-----------book page break-----------
We can have lines that meet on the other side also, as shown in the figure below:
Now, let us look at Figure-4 shown below:

What happens when these lines are extended on either side? You can extend these lines indefinitely but they will never meet. These lines are called $\underline{parallel\ lines}$.
When two lines on a given plane are not, parallel to each other, they are called $\underline{intersecting\ lines}$
-----------book page break-----------
If two lines $AB$ and $CD$ are parallel to each other, they are written as $AB \parallel CD$, while, if $AB$ and $CD$ are not parallel, that is, they are intersecting, then they are shown as $AB \nparallel CD$
II. Properties Of Parallel Lines
The following properties of parallel lines are commonly used in mathematics:
- The distance between two parallel lines remains
constant
, no matter how much you move towards either side.- The distance between two intersecting lines
decreases
as you move towards the intersection point, and increases
as you move away from the intersection point.- If a third line is parallel to any one of a given pair of parallel lines, then it is parallel to the other line also.
- If If a third line intersects any one of a given pair of parallel lines, then it intersects the other line as well.
III. Transversal
To understand what a transversal is, let us draw a pair of parallel lines $p$ and $q$ and a third line $t$ that cuts through (intersects) the two parallel lines. as shown below:
-----------book page break-----------
In this case, the line $t$ which cuts through parallel lines $p$ and $q$, is called the $\underline{transversal}$.
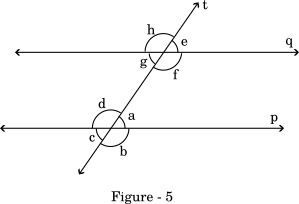
The two intersections of the transversal line with the given pair of parallel lines give us $8$ angles, marked $a$ to $h$, whose properties we will see in the following section.
IV. Angles Formed By Parallel Lines and A Transversal
Now that we know what parallel lines and transversals are, let us look at the angles formed by these lines and their relations. The widget below shows the names of various angles and their relations. (Maximize the widget for more clarity).
If we look at the points of intersections, then the intersection point of the transversals and line $p$ gives us angles $a$, $b$, $c$, $d$ and the intersection point of the transversal with line $q$ gives us angles $e$, $f$, $g$, $h$.
-----------book page break-----------
V. Summary
Let's summarize what we learnt till now. We will refer to Figure-5 for these postulates.
$Corresponding\ Angles$
In the referred Figure-5 the corresponding angle pairs are:
$\angle a$ and $\angle e$
$\angle a$ and $\angle e$
$\angle b$ and $\angle f$
$\angle d$ and $\angle h$
$\angle c$ and $\angle g$
As we saw in the widget above, $\underline{\text{Corresponding angles are equal}}$
$Alternate\ Interior\ Angles$
In Figure-5 the alternate interior angle pairs are:
$\angle a$ and $\angle g$
$\angle d$ and $\angle f$
As we saw in the widget above, $\underline{\text{Alternate interior angles are equal}}$
$Alternate\ Exterior\ Angles$
In Figure-5 the alternate exterior angle pairs are:
$\angle b$ and $\angle h$
$\angle c$ and $\angle e$
As we saw, $\underline{\text{Alternate exterior angles are equal}}$
Combining this and the previous axiom, we can also say $\underline{\text{Alternate exterior angles are equal}}$
-----------book page break-----------
$Consecutive\ Interior\ Angles$
In Figure-5 the consecutive interior angle pairs are:
$\angle a$ and $\angle f$
$\angle d$ and $\angle g$
As we saw in the widget above, $\underline{\text{Consecutive interior angles sum up to } 180^\circ}$
Now, let us try the examples in the following section.
VI. Examples
$\underline{\text{Example - 1}}$:
--------- Reference to question: 5da27cc8-2d8d-4ebd-9e5c-c06b92ced866 ---------
-----------book page break-----------
$\underline{\text{Example - 2}}$
--------- Reference to question: 5e6c9ce3-bba5-449a-9b1f-58c2ab5fe952 ---------