Stewart's Theorem

$\underline{Definition:}$

$Cevian$ is the general term used for any line segment drawn from any vertex of a triangle to the opposite side. By that definition, the medians, the angle bisectors, altitudes are cevians. However, the perpendicular bisectors are not always cevians.

$\underline{Theory:}$

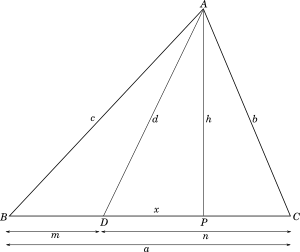
For any $\triangle ABC$, if a cevian $AD$, of length $d$, divides the opposite side $BC$ into two parts, $m$ and $n$ respectively, then:

$b^2m + c^2n = a(d^2 + mn)$, where $a,\ b,\ c$ are the lengths of the three sides $BC$, $CA$ and $AB$ respectively.

$\underline{Construction:}$

In $\triangle ABC$ with side lengths $a,\ b,\ c$, let $D$ be a point on $BC$ such that $BD = m$, $DC = n$.

-----------book page break-----------

Altitude $AP$ is drawn to $BC$.

Let $DP = x$

$\underline{Proof:}$

Considering right-angled $\triangle APD$,

$d^2 = h^2 + x^2$

Considering $\triangle APC$

$b^2 = h^2 + (n - x)^2$

$\Rightarrow b^2m = h^2m + m(n-x)^2$

$\Rightarrow b^2m = h^2m + mn^2 - 2mnx + mx^2$

Considering $\triangle APB$

$c^2 = h^2 + (m + x)^2$

$\Rightarrow c^2n = h^2n + n(m + x)^2$

$\Rightarrow c^2n = h^2n + nm^2 + 2mnx + nx^2$

Therefore,

$b^2m + c^2n = h^2m + mn^2 - 2mnx + mx^2 + h^2n + nm^2 + 2mnx + nx^2$

$\Rightarrow b^2m + c^2n = h^2m + h^2n + mx^2 + nx^2 + nm^2 + mn^2$

$\Rightarrow b^2m + c^2n = h^2(m + n) + x^2(m + n) + mn(m + n)$

$\Rightarrow b^2m + c^2n = (m + n)(h^2 + x^2 + mn)$

Substituting $m + n = a$ and $h^2 + x^2 = d^2$

$b^2m + c^2n = a(d^2 + mn)$

-----------book page break-----------

$\underline{Corollary\ 1:}$

If $AD$ is a median of $\triangle ABC$, of length $d$, then:

$2d^2 = b^2 + c^2 - \dfrac{a^2}{2}$

Using the generic case for a cevian, when the cevian is a median, we have:

$m = n = \dfrac{1}{2}a^2$

From Stewart's Theorem, we know:

$b^2m + c^2n = a(d^2 + mn)$

$\therefore \dfrac{b^2a}{2} + \dfrac{c^2a}{2} = a\left(d^2 + \dfrac{a^2}{4}\right)$

$\Rightarrow \dfrac{b^2}{2} + \dfrac{c^2}{2} = \left(d^2 + \dfrac{a^2}{4}\right)$

$\Rightarrow b^2 + c^2 = 2d^2 + \dfrac{a^2}{2}$

$\Rightarrow 2d^2 = b^2 + c^2 - \dfrac{a^2}{2}$

$\underline{Corollary\ 2:}$

$\unicode{0x201C}$The sum of the squares of the distances of a triangle from the vertices is equal to one-third the sum of the squares of the sides.$\unicode{0x201D}$

Let $m_a,\ m_b,\ m_c$ be the three medians to sides $a$, $b$ and $c$ respectively.

-----------book page break-----------

Using $Corollary\ 1$, we get:

$2m_a^2=b^2+c^2-\dfrac{1}{2}a^2$

$2m_b^2=a^2+c^2-\dfrac{1}{2}b^2$

$2m_c^2=a^2+b^2-\dfrac{1}{2}c^2$

Adding the three equations above, we get:

$2m_a^2+2m_b^2+2m_c^2=b^2+c^2-\dfrac{1}{2}a^2+a^2+c^2-\dfrac{1}{2}b^2+a^2+b^2-\dfrac{1}{2}c^2$

$\Rightarrow 2m_a^2+2m_b^2+2m_c^2=\dfrac{3}{2}a^2+\dfrac{3}{2}b^2+\dfrac{3}{2}c^2$

$\Rightarrow2(m_a^2+m_b^2+m_c^2)=\dfrac{3}{2}(a^2+b^2+c^2)$

$\Rightarrow m_a^2+m_b^2+m_c^2=\dfrac{3}{4}(a^2+b^2+c^2)$

$\Rightarrow\dfrac{4}{9}(m_a^2+m_b^2+m_c^2)=\dfrac{1}{3}(a^2+b^2+c^2)$

$\Rightarrow\left(\dfrac{2}{3}m_a\right )^2+\left(\dfrac{2}{3}m_b\right) ^2+\left(\dfrac{2}{3}m_c\right )^2=\dfrac{1}{3}(a^2+b^2+c^2)$

$\therefore$ The sum of the squares of the distances of a triangle from the vertices is equal to one-third the sum of the squares of the sides.