Euler Line

$\underline{Theory:}$

The orthocentre, circumcentre and the centroid of a triangle lie on the same line, namely the $Euler\ Line$.

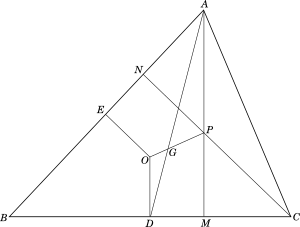
Given $\triangle ABC$, $D$, $E$ the midpoints of $BC$ and $AB$ respectively, $AD$ the median from $A$ and $O$ and $G$ the circumcentre and centroid respectively, of $\triangle ABC$

$\underline{Construction:}$

Lines $OE$ and $OD$ are drawn. Since $O$ is the circumcentre, $OE$ and $OD$ are perpendicular bisectors of $AB$ and $BC$ respectively. $OG$ is extended to $P$ such that $OG=\dfrac{1}{2}GP$ and extend $AP$ and $CP$ to intersect $BC$ and $AB$ at $M$ and $N$ respectively.

-----------book page break-----------

$\underline{Proof:}$

As $AD$ is the median of $\triangle ABC$, and $G$ is the centroid,

$\dfrac{AG}{GD}=\dfrac{2}{1}$

By construction,

$\dfrac{GP}{OG}=\dfrac{2}{1}$

$\dfrac{AG}{GD}=\dfrac{GP}{OG}=\dfrac{2}{1}$

$\angle OGD = \angle PGA$

$\therefore \triangle AGP \sim \triangle DGO$ (using SAS rule of similarity)

$\therefore \angle ODG = \angle PAG$

$\therefore AP\parallel OD$ (alternate angles are equal)

As $OD \perp BC$ and $AP\parallel OD ,$

$AM \perp BC$

Similarly, we can join $CE$, and show that $CN \perp AB$.

$\therefore P$ is the intersection point of the altitudes $AM$ and $CN$ and is the orthocentre.

$\therefore$ The circumcentre,centroid and the orthocentre are collinear. This line is called the Euler Line.

$\underline{Corollary\ 1:}$

The distance of the circumcentre $(O)$ from centroid $(G)$ and the distance of the orthocentre $(P)$ from the centroid are in the ratio $1:2$.

-----------book page break-----------

$\underline{Corollary\ 2:}$

$OG^2=R^2-\dfrac{1}{9}(a^2+b^2+c^2)$ where $R$ is the circumradius of $\triangle ABC$

Let $M$ be any point inside $\triangle ABC$, with centroid $G$, medians $AA'$, $BB'$ and $CC'$ and let $D$ be the midpoint of $AG.$

$MA'\ ,\ MG$ and $MD$ are the medians of $\triangle s\ MBC,\ MDA'$ and $MAG$ respectively, as shown in the figure below:

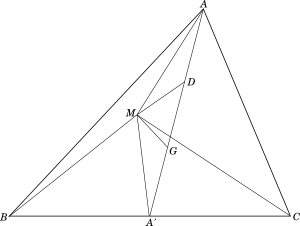
Applying the formula for medians from $Corollary\ 1$ of Stewart's Theorem explained , we get:

$MB^2+MC^2=2MA'\ ^2+\dfrac{1}{2}BC^2$ $...eqn\ (i)$

$MD^2+MA'\ ^2=2MG^2+\dfrac{1}{2}DA'\ ^2$ $...eqn\ (ii)$

$MA^2+MG^2=2MD^2+\dfrac{1}{2}AG^2$ $...eqn\ (iii)$

-----------book page break-----------

Since $G$ and $D$ are the midpoints of $A'D$ and $GA$ respectively, $DA' = AG$.

Substituting $DA' = AG$ in $eqn\ (ii)$ and multiplying it by $2$, then adding all three equations we get:

$MB^2+MC^2+2MD^2+2MA'\ ^2+MA^2+MG^2$

$=2MA'\ ^2+\dfrac{1}{2}BC^2+4MG^2+AG^2 +MA^2+MG^2$

$=2MD^2+\dfrac{1}{2}AG^2$

$\Rightarrow MA^2+MB^2+MC^2-3MG^2=\dfrac{1}{2}BC^2+\dfrac{3}{2}AG^2$

Doing the same for the medians $BB'$ and $CC'$, we get two more equation, which when added to our previous equation gives-

$3(MA^2+MB^2+MC^2-3MG^2)$

$=\dfrac{1}{2}(BC^2+CA^2+AB^2)+\dfrac{3}{2}(GA^2+GB^2+GC^2)$

From $Corollary\ 2$ of Stewart's Theorem, we know that,

$BC^2+CA^2+AB^2=3(GA^2+GB^2+GC^2)$

Substituting $BC^2+CA^2+AB^2=3(GA^2+GB^2+GC^2)$, in the above equation, we get,

$3(MA^2+MB^2+MC^2-3MG^2)=BC^2+CA^2+AB^2$

When $M$ is the circumcentre $O$ we get,

$3(MA^2+MB^2+MC^2-3MG^2)=BC^2+CA^2+AB^2$

$\Rightarrow3(OA^2+OB^2+OC^2-3OG^2)=BC^2+CA^2+AB^2$

$\Rightarrow 3(R^2+R^2+R^2-3OG^2)=BC^2+CA^2+AB^2$

-----------book page break-----------

$\Rightarrow 3(3R^2-3OG^2)=BC^2+CA^2+AB^2$

$\Rightarrow 9R^2-9OG^2=BC^2+CA^2+AB^2$

$\Rightarrow 9R^2-9OG^2=a^2+b^2+c^2$

$\Rightarrow OG^2=R^2-\dfrac{1}{9}(a^2+b^2+c^2)$