Angles By Clock Hands

We saw how to calculate the values of entities that are dependent on other entities. Today we will understand a very specific application of this method.

We know that the hour hand of a clock hand rotates by $360^o$ in $12$ hours. Therefore, the hour hand rotates by $\dfrac{360}{12} = 30^o$ every hour.

We also know that every hour the minute hand rotates by $360^o$

We need to remember a couple of things while we solve these types of problems:

- At any hour and $00$ minutes, the hour hand is at the hour angle, and the minute hand is exactly at $12\ o'clock$ position

- For any amount of time after that, both the hour hand and the minute hand would rotate by some amount.

- To find the angle between the hour and and the minute hand we can find out the angles formed with the $12\ o'clock$ position by both hands and take the difference.

For example:

What is the angle between the hour and the minute hands at $2:05\ pm$?

We know that at $2:00\ pm$ the angle between the $12\ o'clock$ position and the hour hand is $60^o$,

and the angle between the minute hand and the $12\ o'clock$ position is $0^o$.

Now, we can find out the angles traversed by each of the hands in $5\ mins$ and then calculate the difference of the two angles to find the angle between them.

The angle traversed by the hour hand in $5\ mins$ is $30 \times \dfrac{5}{60} = \dfrac{5}{2} = 2.5^o$

So the angle between the hour hand and the $12\ o'clock$ position is $60^o + 2.5^o = 62.5^o$

-----------book page break-----------

The angle traversed by the minute hand in $5\ mins$ is $30^o$.

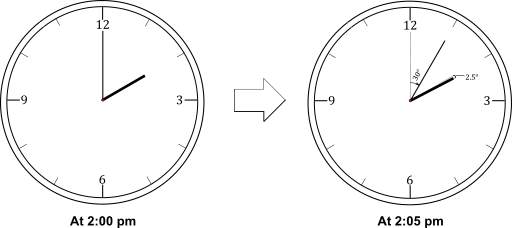
So, the angle between the minute hand and the $12\ o'clock$ position will be $0^o + 30^o = 30^o$

The angle between the two hands will be $62.5^o - 30^o = 32.5^o$

Let us take another example:

What is the angle between the hour and the minute hand at $2:30\ pm$?

As the previous problem we know that, at $2:00\ pm$, the angle between the hour hand and the $12\ o'clock$ position is $60^o$

In $30\ mins$ the hour hand will rotate by $30 \times \dfrac{30}{60} = 15^o$

Hence, the angle between the $12\ o'clock$ position and the hour hand is $60 + 15 = 75^o$

-----------book page break-----------

In $30\ mins$ the minute hand will rotate by $360 \times \dfrac{30}{60} = 180^o$

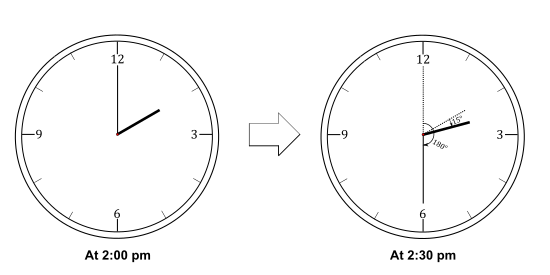
Hence, the angle between the hour and the minute hand at $2:30\ pm$ is $180 - 75 = 105^o$