Understanding The Hyperbola
I. Introduction
Hyperbola is a , which exists in form of two disjoint smooth curves. It is formed when the angle of the plane cutting the double napped cone ($\beta$) is less than the angle of the generator of the cone ($\alpha$) with the axis of the cone. Each of the two parts of the curve is a mirror image of the other, and is open on one side.
II. Hyperbola As Locus
Like , hyperbola can be defined in two ways using the locus of a point on a plane.
- It is the locus of a point such that the absolute difference of distances of the point from two given fixed points is a constant.
- It is the locus of a point such that the ratio of the distance of the point from a given fixed point, called the $focus$ and and the distance from a given fixed line, called the directrix, is a constant $ \gt 1$ called the $eccentricity$
Since for the ellipse we used the first definition to derive the equation, here we will use the second definition to derive our equation and leave it to the reader to derive it from the first form.
Let us start by selecting any point $F$ as the focus on the $x$-axis, and the directrix as a line perpendicular to the $x$-axis intersecting the $x$-axis at $D (d, 0)$, to the right of $F$.
Let point $P$ divide the $FD$ segment in ratio $e:1$ internally, and the point $P'$ divide the segment $FD$ externally in the ratio $e:1$
-----------book page break-----------
Therefore, the points $P$ and $P'$ satisfy the condition:
$\dfrac{PF}{PD} = e$ and
$\dfrac{P'F}{P'D} = e$.
Therefore, both $P$ and $P'$ lie on the hyperbola as per the second definition of hyperbola given above.
Let us take the distance between $P$ and $P'$ as $2a$, and the midpoint of the segment $PP'$ as the origin $O$ and draw the $y$-axis through it, as shown in the following diagram, which gives us the coordinates of $P$ and $P'$ as $(a, 0)$ and $(-a, 0)$:
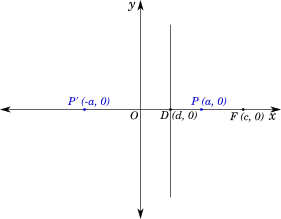
Let the coordinates of $F$ be $(c, 0)$.
-----------book page break-----------
$\because \dfrac{PF}{PD} = e$
$\Rightarrow \dfrac{PF}{a - d} = e$
$\Rightarrow PF = ea - ed$ $...eqn(i)$
Similarly,
$\because \dfrac{P'F}{P'D} = e$
$\Rightarrow \dfrac{P'F}{a + d} = e$
$\Rightarrow P'F = ea + ed$ $...eqn(ii)$
Subtracting $(ii)$ from $(i)$,
$P'F - PF = 2ed$
$\Rightarrow P'P = 2ed$
Since $P'P = 2a$, we get:
$2a = 2ed$
$\Rightarrow d = \dfrac{a}{e}$ $...eqn(iii)$
From the diagram, $PF = c - a$
Therefore,$\dfrac{c-a}{a - d} = e$
$\Rightarrow c - a = e(a - d)$
Substituting the value of $d$ from $eqn(iii)$
$\therefore c - a = e\left(a - \dfrac{a}{e}\right)$
$\Rightarrow c - a = ea - a$
$\Rightarrow c = ea$
-----------book page break-----------
Now we are ready to find the locus of any generic point $P (x, y)$ such that its distance from the focus $F$ and from the directrix is in the fixed ratio $e$
Observe that the directrix is a line perpendicular to the $x$-axis, at a distance of $\dfrac{a}{e}$ from the origin, therefore, has the equation of $x = \dfrac{a}{e}$, and the distance of any point $P(x, y)$ from this line will be $|x - \dfrac{a}{e}|$
Therefore, applying the condition of the locus, we get:
$\dfrac{\sqrt{(x - c)^2 + y^2}}{|x - \dfrac{a}{e}|} = e$
$\dfrac{(x - c)^2 + y^2}{\left(x - \dfrac{a}{e}\right)^2} = e^2$
$\Rightarrow (x - c)^2 + y^2 = e^2\left(x - \dfrac{a}{e}\right)^2$
$\Rightarrow (x - ea)^2 + y^2 = e^2\left(x - \dfrac{a}{e}\right)^2$
$\Rightarrow x^2 - 2eax + e^2a^2 + y^2 = e^2\dfrac{(ex - a)^2}{e^2}$
$\Rightarrow x^2 - 2eax + e^2a^2 + y^2 = e^2x^2 - 2eax + a^2$
$\Rightarrow e^2x^2 - x^2 - y^2 = e^2a^2 - a^2$
$\Rightarrow x^2(e^2 - 1) - y^2 = a^2(e^2 - 1)$
-----------book page break-----------
$\Rightarrow \dfrac{x^2(e^2 - 1)}{a^2(e^2 - 1)} - \dfrac{y^2}{a^2(e^2 - 1)} = 1$
$\Rightarrow \dfrac{x^2}{a^2} - \dfrac{y^2}{a^2(e^2 - 1)} = 1$
Since, $a$ and $e$ are constants, we can substitute $a^2(e^2 - 1) = b^2$ where $b$ is a constant, and get:
$\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$
which is the standard form of hyperbola, with its center at the origin, the focii on the $x-axis$ and the directrix parallel to the $y$-axis.
Observe, that in the following diagram, there will be one more set of points $D' (-d, 0)$ and $F' (-c, 0)$ to the left of the center $O$, which will satisfy the condition of the locus for the same points $P$ and $P'$.
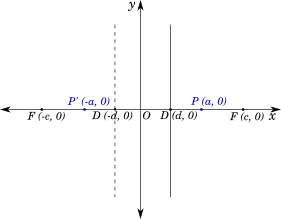
-----------book page break-----------
Therefore, an hyperbola will have a pair of focii, equidistant from the center, with each focus having a corresponding directrix.
We encourage the reader to derive the equation of the hyperbola using the second definition of the locus given at the beginning of this section. The method would be similar to the one we adopted for deriving the standard equation for ellipse.
Now that we have one derivation of the equation of a hyperbola, you can experiment a little with the following widget and try to develop a better feeling of how the various parameters of a hyperbola are related to each other.
-----------book page break-----------
III. Definitions Related To Hyperbola
In the previous section we saw some of the definitions related to hyperbola. Here we will summarize the relevant definitions. For all our definitions we will use the hyperbola in its standard form, that is $\dfrac{(x - x_0)^2}{a^2} - \dfrac{(y - y_0)^2}{b^2} = 1$, where $(x_0, y_0)$ is the center of the hyperbola.
Transverse Axis: A line joining the two focii, passes through the two vertices of the hyperbola. The line segment between these two vertices is called the transverse axis. In the standard form of equation, the length of the transverse axis is $2a$.
Conjugate Axis: The line passing through the centre of the hyperbola and perpendicular to the transverse axis is called the conjugate axis. Using the standard form of equation, the length of the conjugate axis is $2b$.
Vertex: The points where the two sections of the hyperbola intersect the major axis, are called the vertices.
Focus: The focii is a pair of points on the major axis at distances of $\pm ea$ from the center.
Directrix: The directrices is a pair of line which are perpendicular to the transverse axis, at distances of $\pm \dfrac{a}{e}$ from the center of the hyperbola, therefore, using the standard form given by the equations $x = \pm \dfrac{a}{e} + x_0$
Eccentricity: The eccentricity, for a given hyperbola, is the ratio of the distance of any point on the hyperbola from any of the focus and from the corresponding directrix.
-----------book page break-----------
For the standard form of equation, the eccentricity can be computed using:
$e = \sqrt{1 + \dfrac{b^2}{a^2}}$
Latus Rectum: The latus rectum is a line segment passing through the focus, perpendicular to the major axis, and terminated on either side by the hyperbola.
Finding the length of a latus rectum from the standard form of the equation is simple.
If we consider a hyperbola of the form $\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$ with the origin as its center and one of its its focii at $(ea, 0)$.
The vertical line passing through this point will be $x = ea$. To find the intersection of this line with the hyperbola, we substitute, $x = ea$ in the equation of the hyperbola and get:
$\dfrac{e^2a^2}{a^2} - \dfrac{y^2}{b^2} = 1$
$\Rightarrow e^2 - \dfrac{y^2}{b^2} = 1$
$\Rightarrow y^2 = b^2(e^2 - 1)$
We know that $b^2 = a^2(e^2 - 1)$ from our original definition of $b^2$ from the derivation, giving us $e^2 - 1 = \dfrac{b^2}{a^2}$
$\therefore y^2 = b^2 \times \dfrac{b^2}{a^2}$
$\Rightarrow y = \pm \dfrac{b^2}{a}$
Therefore, the latus rectum intersects the hyperbola at $\left(\dfrac{b^2}{a}, 0\right)$ and $\left(-\dfrac{b^2}{a}, 0\right)$ and its length is $\dfrac{b^2}{a} - \left(-\dfrac{b^2}{a}\right) = \dfrac{2b^2}{a^2}$.
-----------book page break-----------
Now it is obvious that if we translate the hyperbola to a different center $(x_0, y_0)$, using the equation $\dfrac{(x - x_0)^2}{a^2} - \dfrac{(y - y_0)^2}{b^2} = 1$, the length of the latus rectum will not change and remain $\dfrac{2b^2}{a^2}$
IV. Other Properties Of Hyperbola
This section will list out a few properties of hyperbola. The proofs of these properties are beyond the scope of this text, but anyhow these properties are interesting enough to know.
Light Property:
Light rays passing through any one of the focii, after reflecting off the concave surface of the hyperbola, will virtually meet at the other focus as shown in the following figure:.
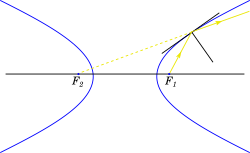
This also implies that the tangent at any point bisects the angle formed by the lines joining that point and the two focii.
-----------book page break-----------
Midpoints Of Parallel Chords:
The midpoints of a set of parallel chords of a hyperbola form the locus of a straight line passing through the center of the hyperbol, as shown in the following figure:

V. Asymptotes Of Hyperbola
In general Asymptote of any curve is a line, whose distance from the curve reduces progressively without ever becoming zero as one move farther away from the origin on the curve. In other words, asymptote is a line whose distance from the curve tends to zero, as the $x$ or $y$ coordinate or both tend to $\pm \infty$. The asymptotes never actually intersects or touches the curve. The asymptotes of an hyperbola have slopes of $\pm \dfrac{b}{a}$ and pass through the center of the hyperbola.
Therefore, the equations of the asymptotes of the hyperbola $\dfrac{(x - x_0)^2}{a^2} - \dfrac{(y - y_0)^2}{b^2} = 1$, which is centered at $(x_0, y_0)$, is given by:
$y - y_0 = \pm \dfrac{b}{a}(x - x_0)$
-----------book page break-----------
For an hyperbola with $b = a$ the slope of the asymptotes will be $+1$ and $-1$, thereby making them perpendicular to each other. These hyperbolas are also called rectangular hyperbola.
There is another special category of rectangular hyperbola of the form $xy = k$, whose asymptotes are the two axes. These hyperbolas can be formed by taking any standard hyperbola centered at the origin and rotating by $45^\circ$
VI. Parametric Form Of Hyperbola
For a hyperbola centered at the origin, the equation becomes $\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = 1$.
Substituting $x = a \sec t$ and $y = a \tan t$ in this equation we get:
$RHS = \dfrac{a^2 \sec^2 t}{a^2} - \dfrac{b^2 \tan^2 t}{b^2}$
$= \sec^2 t - \tan^2 t$
$= 1 = LHS$
Since the above substitution satisfies the equation for all values of $t$ other than $t = \dfrac{\pi}{2}$, the parametric form of hyperbola can be:
$x = a \sec t$
$y = b \tan t$ where $t \ne \dfrac{\pi}{2}$