Apportioning Line Segments
Today we will see how to find a point on any given line segment such that the point divides the line in any given ratio $m:n$
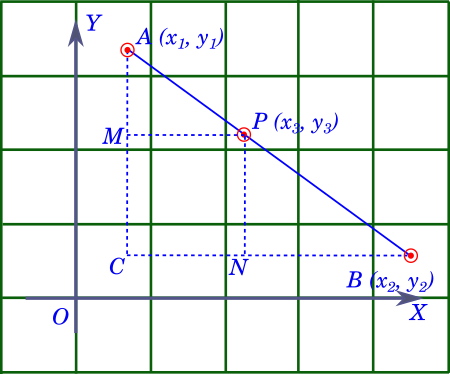
Let's say that $A\ (x_1, y_1)$ and $B\ (x_2, y_2)$ are two distinct points on the Cartesian plane.
We need to find the coordinates of a on $AB$ such that it divides the line in the ratio $m:n$
Let us draw line segment $AB$, and let point $P\ (x_3,\ y_3)$ be the point which divides the line $AB$ in the ratio $m:n$, as shown in the figure below.
We need to find $x_3, y_3$ in terms of $x_1$, $y_1$, $x_2$, $y_2$, $m$ and $n$.
-----------book page break-----------
Let us draw lines parallel to the $X$ and $Y$ axis from points $A$, $B$ to form right angled triangle $ABC$ with $AB$ as the hypotenuse, as shown in the above figure.
Let point $P\ (x_3,\ y_3)$ be the point which divides the line $AB$ in the ratio $m:n$. We need to find $x_3, y_3$ in terms of $x_1$, $y_1$, $x_2$, $y_2$, $m$ and $n$.
From point $P$ draw lines parallel to the two axes to meet $AC$ and $BC$ at $M$ and $N$ respectively.
Let us list out the coordinates of the new points that we have drawn in the above figure.
The coordinates of $C$ is $x_1,\ y_2$ $\because AC \parallel Y$ axis and $BC \parallel X$ axis, $C$ will have the $X$ coordinate same as $A$ and $Y$ coordinate same as $B$
The coordinates of $M$ is $x_1,\ y_3$ $\because PM \parallel X$ axis, all points on $PM$ will have the same $Y$ value
Similarly, the coordinates of $N$ is $x_3,\ y2$
Consider $\triangle s$ $APM$ and $ABC$
$\because PM \parallel BC$, $\triangle APM \sim ABC$
$\therefore \dfrac{AP}{PB} = \dfrac{AM}{MC}$
$\therefore \dfrac{y_3 - y_1}{y_2 - y_3} = \dfrac{m}{n}$
$\Rightarrow ny_3 - ny_1 = my_2 - my_3$
$\Rightarrow ny_3 + my_3 = my_2 + ny_1$
$\Rightarrow y_3(m + n) = my_2 + ny_1$
$\Rightarrow y_3 = \dfrac{my_2 + ny_1}{m + n}$
-----------book page break-----------
Similarly, considering $\triangle s$ $BAC$ and $BPN$, we get:
$\dfrac{AP}{PB} = \dfrac{CN}{NB}$
$\therefore \dfrac{x_3 - x_1}{x_2 - x_3} = \dfrac{m}{n}$
$\Rightarrow nx_3 - nx_1 = mx_2 - mx_3$
$\Rightarrow nx_3 + mx_3 = mx_2 + nx_1$
$\Rightarrow x_3(n + m) = mx_2 + nx_1$
$\Rightarrow x_3 = \dfrac{mx_2 + nx_1}{m + n}$
-----------book page break-----------
Let us try the following example:
--------- Reference to question: 6c5fb12f-e48c-4c98-b21f-19c84697fb58 ---------
-----------book page break-----------
Now, let us try one more example:
--------- Reference to question: 1a1cf1a3-0fbe-4070-a899-862209400ea5 ---------