Introduction To Extrema


I. Introduction To Local Extrema
Take a look at the function plot shown below. The gray line is a tangent to $f(x)$ at any given point $P$. Try dragging $P$ along the curve to see how the slope of the tangent changes along various points on the curve. 

--------- Reference to widget: 9038e649-0b27-43ab-9514-90c2bf1adee2 ---------

You will observe that the points at which the slope is $0$, that is the tangent is parallel to the $x$-axis, that point is either the minimum or the maximum in that region.

-----------book page break-----------
In other words, the given point is greater than its neighbouring points on both sides (for local maxima) or the point is less than its neighbouring points on both sides (for local minima).
These points are called the extrema (singular: extremum) of the function $f(x)$.

It is evident from our experiment with the previous widget that if a function is differentiable in a given range where there is an extrema, then the derivative (slope) of the function will be equal to $0$ at the extrema, that is:
$slope = \dfrac{d}{dx} f(x) = 0$ 

Therefore, for these cases, we can find the extrema of a function by equating the first derivative to $0$, and solving for all possible values of $x$.
There can be another type of extrema, where the derivative of the function does not exist at a given point $P$ but the assertion that the neighbouring points before and after this point are all greater than or less than the given point holds true.
Let us take a look at the plot of the function $f(x) = |\sin x|$ shown below:


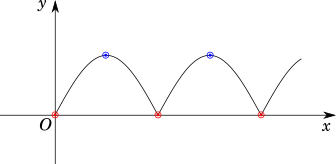
Each of the blue points is a maxima, and each of the red points is a minima, because both the blue points satisfy the condition of being greater than the neighbouring points in that region, and the red points satisfy the condition of being lesser than its neighbouring points.

-----------book page break-----------
However, as we saw , the first derivative of the function $\dfrac{d}{dx} |\sin x|$ at the red points does not exist. But, the red dotted points satisfy the condition $f(x - \delta x) > f(x)$ as well as $f(x + \delta x) > f(x)$ for all $\delta x \lt \epsilon$ for some arbitrarily small $\epsilon$.

II. Critical Points
At any point $x$, if the value of $f'(x)$ is $0$ or does not exist is called a critical point of the function. 
The diagram below shows the plot of the function:
$f(x) = \left\{\begin{array}{ll} -x + 5 & \text{for } x \le 2 \\ \dfrac{6}{x} & \text{for } x \gt 2 \end{array}\right.$

Point $P = (2, 3)$ is a critical point of $f(x)$, is it also an extremum of $f(x)$?



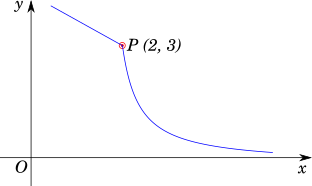
The answer is No. It is evident from the figure that for points to the left of $P$, $f(x) \gt 3$ and for points to the right of $P$, $f(x) \lt 3$.

-----------book page break-----------
 Now try the following problem:

--------- Reference to question: 9d3a6f9c-ff0b-4ba5-856e-68b45b6bd473 ---------


In the next section we will see how to distinguish between a local maximum and a local minimum.

-----------book page break-----------
III. Distinguishing Between Maxima & Minima:
Let us look at the plot of the same function we saw in the first page. Here the plot is marked with all the visible maxima (green) and minima (yellow).
Click on any of the maxima or minima to see how the slope of the curve varies around these points.

--------- Reference to widget: 9e4b565f-b3ce-405d-b933-3ea0d86446a0 ---------


The green curve, which is plotted as point $P$ moves along the curve of $f(x)$, is the plot of the first derivative $f'(x)$. You can see that the plot of $f'(x)$ intersects the $x$-axis at the point of the extrema. We saw this before, that if, the derivative $f'(x)$ exists, then, at every extrema $f'(x) = 0$.

-----------book page break-----------
Let us look us what happens around the extrema, starting just before the extrema and ending just after the extrema (the region shaded in green when you click a point). If you try this at any of the maxima, then you will observe that $f'(x)$ is a reducing function in this range, and for any of the minima, $f'(x)$ is an increasing function.
We can analyse the case of a maxima. Click the point $A_1$ in the previous widget, then try to drag point $P$ from the left end of the green shaded region to the right end of this region. You will observe that the tangent rotates clockwise from a positive slope to $0$, then further to a negative slope.
If you look at the graph of $f'(x)$ this is confirmed, that is $f'(x)$ reduces from a positive value at the left to a negative value at the right boundary.
Therefore, $f'(x)$ is a reducing value from left boundary to the right boundary, and has a negative slope.
Therefore, $f''(x)$ will be negative in this region.
Applying similar logic and experimenting with any of the minima, you will see that the slope of $f'(x)$ is positive in the region containing the minima.
Therefore, $f''(x)$ in this case will be positve.
Therefore, we can use the sign of the second derivative $f''(x)$ to decide whether a given extremum is a minimum or a maximum.

What happens when the both the first and the second derivatives of a function become $0$ at any point?

-----------book page break-----------
Let us look at the plot of a simple function $f(x) = (x - 4)^3 + 1$ as shown below:


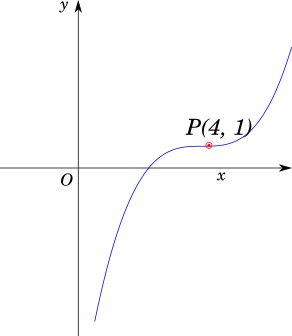
The first derivative, $f'(x) = \dfrac{d}{dx} f(x) = 3(x-4)^2$.
At $x = 4$, $f'(x) = 0$ therefore, $x = 4$ is a critical point of $f(x)$

The second derivative $f''(x) = \dfrac{d}{dx} f'(x) = 6(x-4)$, is also equal to $0$ at $x = 4$. Therefore, $x = 4$ is neither a local maximum nor a minumum for $f(x)$.

-----------book page break-----------
It can be visualised from the above figure, that the slope of $f(x)$ keeps reducing till $x = 4$ and after $x = 4$ it continues to grow positive.
The slope, $f'(x)$ never crosses from a positive value to a negative value or vice versa, therefore this function does not have a finite maximum or minimum. 

Now we can summarize the concept of maxima and minima.
- A function can have one or more extrema.

- When there are more than one extrema, it is always the case that a minima is followed by a maxima and vice versa. No two maxima or minima can occur in succession.

- A function is increasing, that is its derivative is positive, between a minima and a succeeding maxima. A function is decreasing between a maxima and the next minima.

- If the derivative of a function exists at an extrema, it has to be equal to $0$.

- If the derivative of a function does not exist at an extrema, then for a minima, the left side slope of $f'(x)$ is negative and the right side slope of $f'(x)$ is positive. Similarly for a maxima the left side slope is positive and the right side slope is negative.

- Every extrema is a critical point, but every critical point is not an extrema.