Lines Dividing A Plane

Here we will see how to count the number of regions generated by a set of straight lines, when no two of them are parallel, and no three of them passes through a common intersection point.

We will see two methods of the derivation here. The first one is based on actual count and finding a pattern.

$\underline{Approach\ 1:}$

Let us start with $0$ lines on the plane. The entire plane is just one region with no bounds.

When we introduce one straight line, which can be extended infinitely it divides the plane into two distinct regions.

When we have two lines intersecting each other, we get $4$ distinct regions as shown in the figure below:

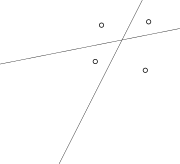
-----------book page break-----------

When we introduce a third line shown below with blue, it will introduce $3$ new regions, each shown with a blue dot as below:

Now when we introduce the fourth line, we get four new regions, as shown with the red dots below. Observe, the no matter how you draw the fourth line, as long as it does not pass through a previously generated intersection point, or is not parallel to any of the existing lines it will always create $4$ new regions.

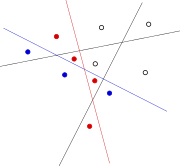
-----------book page break-----------

Now, it is easy to see the pattern.

We started with $0$ lines and $1$ region.

When we introduced the $1\xasuper{st}$ line we got $1$ new region, to get a total of $2$ regions.

When we introduced the $2\xasuper{nd}$ line we got $2$ new regions, to get a total of $4$ regions.

When we introduced the $3\xasuper{rd}$ line we got $3$ new regions, to get a total of $7$ regions.

When we introduced the $4\xasuper{th}$ line we got $4$ new regions, to get a total of $11$ regions.

Similarly when we introduce the $n\xasuper{th}$ line we will get $n$ new regions.

Therefore, if we denote the number of regions formed by $n$ lines as $S_n$, and when we introduce the $(n+1)\xasuper{th}$ line, we will get $n + 1$ new regions, therefore,

$S_{n+1} = S_n + (n + 1)$ or alternately we can also say:

$S_n = S_{n-1} + n$

Therefore,

$S_n = n + S_{n-1}$

$= n + (n - 1) + S_{n - 2}$

$= n + (n - 1) + ... + (1 + S_0)$ where $S_0$ is the number of regions formed by $0$ lines which we know is $1$

$\therefore S_n = n + (n - 1) + ... + 1 + 1 = \dfrac{n(n+1)}{2} + 1 = \xacomb{n+1}{2} + 1$

-----------book page break-----------

$\underline{Approach\ 2:}$

To understand this approach, along with the conditions that no two lines are parallel and no three lines intersect at the same point, we will also assume that there is no line that is horizontal. It is easy to see why this additional condition does not alter the number of regions formed.

Because if we have a horizontal line, then all we need to do is rotate the whole plane to make the line inclined and this will not change the number of regions. But this assumption will greatly ease the visualisation of the problem.

Since, no line is horizontal, this means that no two intersection points lying on the same line is at the same height.

Since there are $n$ lines, each line intersecting with every other line at distinct points, there are $\xacomb{n}{2}$ points.

Each of these points will form the bottom most vertex of exactly one region, as shown below:

-----------book page break-----------

Since there are $\xacomb{n}{2}$ points, there are $\xacomb{n}{2}$ regions that are bounded below by one of these points.

Other than these there are some regions which are open at the bottom and does not have a lowest point. How many such regions are there?

We can find this by introducing a horizontal line $l$ as shown below

-----------book page break-----------

This new line will be intersected exactly at $n$ points by the previous $n$ lines, therefore will be divided into $n + 1$ parts. Each of these parts will belong to a region which was previously open at the bottom. Therefore, before this line was introduced, that is with $n$ lines, there were $n + 1$ parts which were open at the bottom.

Therefore, with $n$ lines, there were a total of $\xacomb{n}{2} + n + 1$ regions.

$\therefore S_n = \xacomb{n}{2} + n + 1$ (we can substitute $n$ with $\xacomb{n}{1}$)

$= \xacomb{n}{2} + \xacomb{n}{1} + 1$

$= \dfrac{n!}{(n-2)!2!} + \dfrac{n!}{(n-1)!1!} + 1$

$= \dfrac{(n-1)n! + n!2}{(n-1)!2!}+ 1$

$= \dfrac{n!(n - 1 + 2)}{(n-1)!2!}+ 1$

$= \dfrac{n!(n + 1)}{(n-1)!2!}+ 1$

$= \dfrac{(n + 1)!}{\left\{(n+1) - 2\right\}!2!}+ 1$

$= \xacomb{n+1}{2} + 1$

Since $1 = \xacomb{n}{0}$ and $n = \xacomb{n}{1}$, in many texts this is directly expressed as $S_n = \xacomb{n}{0} + \xacomb{n}{1} + \xacomb{n}{2}$