Polygons And Lines Of Symmetry
I. What Are Polygons?
A polygon is a figure surrounded on all sides by straight lines. The points at which any two adjacent sides meet, forms a corner and is called a $vertex$ (plural: $vertices$). A polygon will have exactly the same number of vertices as it has sides.
A $3$ sided polygon is called a triangle, a $4$ sided polygon is called a quadrilateral, a $5$ sided polygon is called a pentagon, and so on.
A polygon, all of whose sides are equal, and so are the angles, is called a
$regular\ polygon$
. Otherwise it is an $irregular\ polygon$
. A regular polygon of $3$ sides is called an
$equilateral$
triangle, which a regular polygon with $4$ sides is a $square$
.A polygon, all of whose corners are pointing outwards, is called a
$convex\ polygon$
. In other words we can say all the angles of a convex polygon are less than a straight angle or $180^\circ$. The below figures are examples of convex polygons: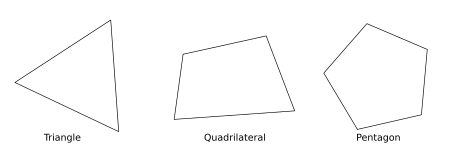
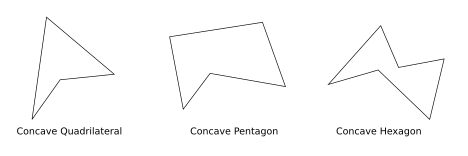
When a polygon has one or more of its corners pointing inwards, it is called a $concave\ polygon$. In other words, at least one of the angles of a concave polygon is more than
$180^\circ$
.-----------book page break-----------
Some concave polygons are shown below:
II. Lines Of Symmetry
Consider an image of an object. If you are able to fold the image along a line through it, such that all the lines and corners of one side of the image falls on the lines and corners of the other side of the image, then you have a line of symmetry.
In the following widget try to find the lines of symmetry for a polygon of your choice folding the polygon using any of its vertices.
-----------book page break-----------
Let us consider the polygon below, which has all sides equal in length:
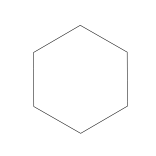
If you draw a line through two of the opposite corners, and fold the drawing as shown below:

After folding your drawing should look like:
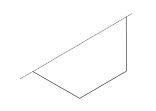
Therefore this is a line of symmetry.
-----------book page break-----------
Likewise if we draw a line through the centres of any two opposite sides, and fold along this line we should get:

Observe that you are getting this because there are an even number of sides. But if the number of sides is odd, you should draw the line of symmetry through a corner and the center of its opposite side to get a line of symmetry like shown below with the $5$ sided figure (pentagon):

For any $n$-sided polygon, there will be $n$ lines of symmetry. For polygons with even number of sides, each pair of opposite vertices, and the midpoints of each pair of opposite sides will give a line of symmetry.
For polygons with odd number of sides, each vertex and the midpoint of the opposite side will give a line of symmetry.
-----------book page break-----------
III. Rotational Symmetry
Now that we have understood lines of symmetry, let us look at one more type of symmetry, which is called rotational symmetry. For this kind of symmetry you will not be folding the given polygon, instead, you will need to rotate the polygon around its center. While rotating the polygon through an angle of $360^\circ$, if you find a position where the polygon looks exactly same as the original polygon, we say that it is a rotational symmetry for the given polygon.
Try the following widget to see if you can find all the points of rotational symmetry for the polygon of your choice.
The total number of points where the rotated polygon looks exactly same as the original polygon, is called the $order\ of\ rotational\ symmetry$
-----------book page break-----------
IV. Line & Rotational Symmetries In Figures Other Than Polygons
Shapes other than regular polygons can also have lines of symmetry or rotational symmetry or both.
Now, try answering the following question.
--------- Reference to question: bd016922-374a-44bf-995d-f46c20d181fa ---------
Polygon Definitions -