Slope Of A Straight Line

We learnt here how to represent linear equations on a Cartesian Plane.

Today we are going to learn more about slopes of a straight line.

$\underline{I.\ Understanding\ Slope}$

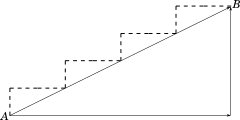
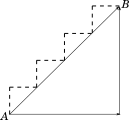
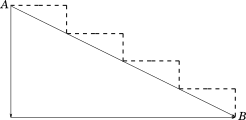
Let us first understand the word $slope$ as we use it in our daily conversation. Take a look at the three diagrams below. Each shows a staircase having the same height, and in each case you are moving from point $A$ to point $B$.

-----------book page break-----------

In the first case, for climbing the same height you would be travelling more horizontal distance as compared to climbing the same height in the second case.

As we can make out easily from the diagram that the second staircase has a steeper slope, or a higher slope than the first.

In the third case as you travel horizontally to the right, you will be going down the slope. In geometry this will be called a negative slope.

Now we have reached a stage where we can define the slope of a line, and it is as follows:

$\unicode{0x201C} The\ slope\ of\ a\ line\ can\ be\ defined\ as\ the\ ratio\ of\ the\ vertical$ $distance\ to\ the\ horizontal\ distance\ when\ moving\ from\ any$ $point\ on\ the\ line\ to\ another\ point\ on\ the\ same\ line \unicode{0x201D}$

We will see in the next section that no matter where you choose the points on a straight line, the slope will always be the same.

$\underline{II.\ Slope\ Of\ A\ Line}$

To understand the slope of a straight line we will start with the example of the equation $y - 2x = 8$

Using the method described , we will plot the line as shown in the following figure:

-----------book page break-----------

Then we will select any two random points $A$ and $B$ on the line. We can move from $A$ to $B$ either by moving along the line, or by moving horizontally to point $P$ and then vertically to point $B$.

$\triangle APB$ is right angled at $P$ with $AP$ parallel to the $X$ axis and $PB$ parallel to the $Y$ axis.

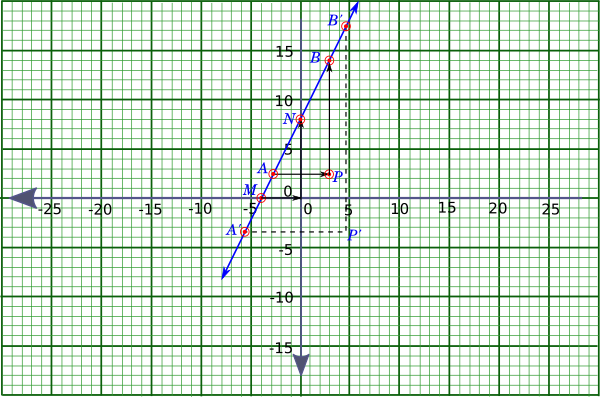
As per our definition the slope of the line is $\dfrac{PB}{AP}$

Instead of moving from point $A$ to $B$, if we had chosen to move from point $A'$ to $B'$ by moving along $A'P'$ and then along $P'B'$, then our slope would be given by $\dfrac{P'B'}{A'P'}$

-----------book page break-----------

Since $AP \parallel A'P$ and $PB \parallel P'B'$,

we can show that $\triangle APB \sim \triangle A'P'B'$

Therefore, based on the similar triangle properties, $\dfrac{PB}{AP} = \dfrac{P'B'}{A'P'}$

Now we can see that no matter where we choose the starting and ending points on the line, our slope value will always be the same.

If the coordinates of points $A$ and $B$ are $x_1, y_1$ and $x_2, y_2$ respectively, then:

$PB = y_2 - y_1$ and $AP = x_2 - x_1$

Therefore, the slope of a line can be calculated given any two points on the line can be calculated using:

$slope = \dfrac{y_2 - y_1}{x_2 - x_1}$

Note that the order in which you take the points is important. Hence if you calculate the slope by using $slope = \dfrac{y_1 - y_2}{x_2 - x_1}$ you will get the incorrect sign of the slope. However, you can take any order of your choice provided you take the same order of points in the numerator and the denominator, that is:

$slope = \dfrac{y_2 - y_1}{x_2 - x_1} = \dfrac{y_1 - y_2}{x_1 - x_2}$

To calculate the slope of the given line, we will choose two points that are easy to calculate. Let us choose the points $M$ and $N$ such that $M$ is the intersection point of the line and the $X$ axis and $N$ is the intersection point of the given line and the $Y$ axis.

-----------book page break-----------

We can find the coordinate of $M$ by putting $y = 0$ in the given equation, and we get:

$0 - 2x = 8$

$\Rightarrow x = -4$

$\therefore$ The coordinate of $M$ is $-4, 0$

Similarly we can find the point $N$ by putting $x = 0$, and get:

$y = 8$

$\therefore$ The coordinate of $N$ is $0, 8$

Therefore, the slope of the given line $ = \dfrac{0 - 8}{-4 - 0} = \dfrac{-8}{-4} = 2$

-----------book page break-----------

$\underline{III.\ Sign\ Of\ A\ Slope}$

In the previous section we learnt about the slope of a line. Now we will see that the slope can either be a positive or a negative value, depending on the line.

If, in moving from one point on a line to another point on the same line, you need to move in both positive $X$ and $Y$ directions or both negative $X$ and $Y$ directions, the slope will be a positive number, as we saw in the example of the previous section.

Whereas, if you have to move in positive $X$ direction, combined with a move in the negative $Y$ direction, or vice versa, the slope will be negative.

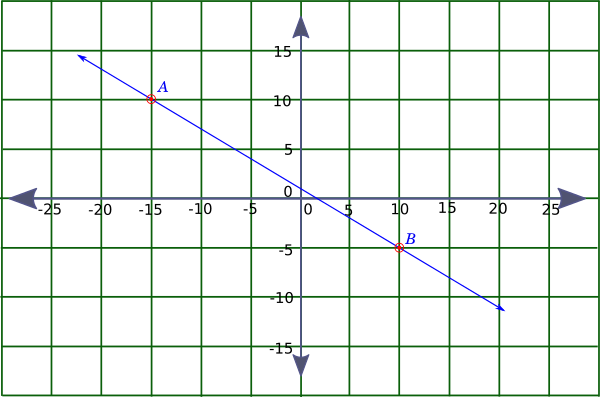
Take the example of the line shown below, which passes through the point $A = (-15,\ 10)$ and $B = (10,\ -5)$

-----------book page break-----------

To find the slope, you can choose to move from either $A$ to $B$ or $B$ to $A$.

To move from $A$ to $B$ you need to move $25$ units in the positive $X$ direction and $20$ units in the negative $Y$ direction.

And the slope becomes $\dfrac{-20}{25} = -\dfrac{4}{5}$

In case you choose to move from $B$ to $A$ you will need to move $25$ units in the negative $X$ direction and $20$ units in the positive $Y$ direction.

Hence, the slope becomes $\dfrac{20}{-25} = -\dfrac{4}{5}$.

So we can see that the sign of the slope and the magnitude depends on the line only and not on the choice of points or on which is your starting point or the ending point.

$\underline{IV.\ Slope\ Of\ A\ Generic\ Linear\ Equation}$

Now, we are ready to find the slope of a generic linear equation of the form $ax + by + c = 0$, directly from the equation, without having to find specific points on the line.

Let's assume for now that $b \ne 0$, $c \ne 0$ and we will see very soon why.

Let us find out the intersection of this line with both the axes.

Let us assume that $c \ne 0$ and the line does not pass through the origin. In that case the line will intersect each of the axes at two distinct point.

Putting $x = 0$ in the equation we get $y = -\dfrac{c}{b}$ and

putting $y = 0$ we get $x = -\dfrac{c}{a}$.

-----------book page break-----------

In the following figure point $A$ is $(-\dfrac{c}{a}, 0)$ and point $B$ is $(0, -\dfrac{c}{b})$

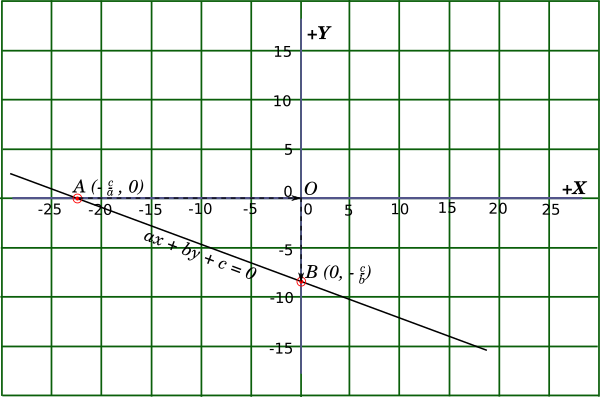
Since we have selected the intersection points of the line with the two axes, the points will form a right angled triangle with the two axes and the origin $O$ as the third point.

Now, if the coordinate of a point is $p, 0$, where $p$ can be either positive or negative, then to move from that point to the origin we will need to move in the direction opposite to the sign of $p$. So, if $p$ is negative we need to move in the positive $X$ direction to reach the origin and if $p$ is positive, we need to move in the negative $X$ direction to reach the origin. Hence, we can say that we need to move $-p$ unit to reach the origin.

-----------book page break-----------

Similarly, if a point has coordinate $0, q$ where $q$ can be either positive or negative, then to reach that point from the origin, we will need to move in the same direction as $q$ is. For example, if $q$ is negative, we need to move in the negative $Y$ direction to reach that point, else, if $q$ is positive, we need to move in the positive $Y$ direction to reach that point from the origin.

Hence, in our case, we can say that to reach from point $A$ to $B$ we need to move by $- \left( - \dfrac{c}{a} \right) = \left( \dfrac{c}{a} \right)$ units along the $X$ axis to reach the origin, and another $\left( - \dfrac{c}{b} \right)$ along the $Y$ axis to reach point $B$ from the origin.

Therefore, the slope of the line will be:

$\dfrac{\left( - \dfrac{c}{b} \right)}{\left( \dfrac{c}{a} \right)}$

$= -\dfrac{a}{b}$

Now we can see the problem that we will have if either $c$ or $b$ equals $0$. In both cases, we will end up with division by $0$ which will give an undefined result. We will see this cases in the later sections.

-----------book page break-----------

$\underline{V.\ Slope\ Of\ Lines\ Passing\ Through\ The\ Origin}$

If in the generic form of linear equation $ax + by + c = 0$, we have $c = 0$, then our equation reduces to:

$by = -ax$ and if we put $x = 0$ we will always get $y = 0$, which means the line passes through the origin.

Now, we can choose the first point as the origin. We can also choose the second point by putting $x = b$ thus getting $y = -a$

Thus our second point becomes $(b, -a)$ and to move from the origin to this point, we need to move $b$ units along the $X$ axis and $-a$ units along the $Y$ axis.Thus we get the slope as $\dfrac{-a}{b}$, which is the same as what we got in the generic case in the previous section.

-----------book page break-----------

$\underline{VI.\ Slope\ Of\ Lines\ Parallel\ To\ Either\ Of\ The\ Axes}$

As we learnt before, the equation of a line parallel to the $X$ axis is given by $y = c$, and we can write this equation in the generic form from the previous section as $0.x + 1.y + (-c) = 0$, and as per the formula of slope derived in the previous section, we get:

$slope = -\dfrac{b}{a} = -\dfrac{0}{1} = 0$

Similarly, any line parallel to the $Y$ axis is given by $x = c$ which can be written as $1.x + 0.y + (-c) = 0$ and as per the formula derived, we get:

$slope = -\dfrac{b}{a} = -\dfrac{1}{0} = undefined$

Therefore, slope of a line parallel to the $X$ axis is always $0$ and the slope of a line parallel to the $Y$ axis is always $undefined$.

-----------book page break-----------

$\underline{VII.\ Finding\ Equation\ Of\ A\ Line\ From\ A\ Point\ \&\ The\ Slope}$

Now let us ask the question, that if we are given the value of a slope can we find the equation of the line?

The answer is $no$, since there can be an infinite number of parallel lines which will have the same slope.

Let us re-state our question, if we are given the coordinates of a point on the line and the slope of the line can we find the equation of the line?

The answer in this case is $yes$. We know that there can be an infinite number of lines passing through any given point, however each one will have a different slope. Since we are given the point and the slope value, we can uniquely identify the line and hence obtain the equation of the line.

Let us say we need to find the equation of a line passing through the point $x_1, y_1$ and having a slope of $s$

Here is how we will proceed.

We know the for all generic points $P = (x,\ y)$ on the line we will have $\dfrac{y - y_1}{x - x_1} = s$

Therefore, our equation becomes:

$y - y_1 = sx - sx_1$

$\Rightarrow y = sx - sx_1 + y_1$

Since $s$, $x_1$ and $y_1$ are given we can find our equation in terms of $x$ and $y$. If any of the values on the right hand side is an irreducable fraction we can multiply both sides by the denominator to obtain the equation in the form $ax + by + c = 0$.

-----------book page break-----------

Let us take an example to better understand this approach:

Find the equation of the line passing through the point $5, 7$ and having a slope of $-\dfrac{2}{3}$

Using our approach, we get:

$\dfrac{y - 7}{x - 5} = -\dfrac{2}{3}$

$\Rightarrow y - 7 = -\dfrac{2}{3}(x - 5)$

$\Rightarrow y = 7 - \dfrac{2x}{3} + \dfrac{10}{3}$

$\Rightarrow 3y = 21 - 2x + 10$

$\Rightarrow 2x + 3y - 31 = 0$