Volume & Surface Area Of Curvilinear 3D Shapes
$\underline{I.\ Sphere}$
A sphere is the simplest of all curvilinear 3D shapes, which is specified by just one dimension, that is the radius.
A sphere can be seen as the collection of all possible points in the 3 dimensional space, that are equidistant from a fixed point, which is the centre of the sphere.
The figure below shows a sphere with center $C$ and radius $r$.
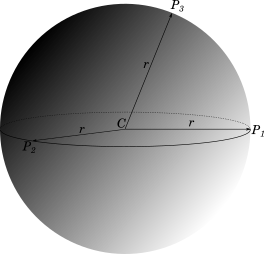
Any point on the circumference, like the examples shown above as $P_1$, $P_2$ and $P_3$ are at a distance $r$ from the centre $C$.
-----------book page break-----------
The surface are of a sphere having radius $R$ is given by $4\pi r^2$ and will have a unit of $length^2$
The volume of a sphere having a radius $R$ is given by $\dfrac{4}{3}\pi r^3$ and will have a unit of $length^3$
Here are a few interesting points about sphere:
- Any plane passing through the centre of the sphere, will divide the sphere into two equal halves called the $hemispheres$.
- Any plane passing through the sphere but not through its centre will divide the sphere into two unequal $spherical\ segments$.
- A cone with its apex at the centre of the sphere, and its base lying on the circumference, will give a $spherical\ cone$.
$\underline{II.\ Cylinder}$
A cylinder is a three dimensional object formed by two parallel circular faces of equal radius, and a curved plane, which is called the lateral surface.
-----------book page break-----------
Given below are the figures of two cylinders.

Both the figures above are circular cylinders. The line $AB$ passing through the centres of the two circular surfaces of each cylinder is called the $\unicode{0x201C}axis\unicode{0x201D}$ of the respective cylinder.
In figure $Figure-2$ above, the axis is at an angle of $90^\circ$ to the circular face. This type of cylinder is called a $\unicode{0x201C}Right\ Circular\ Cylinder\unicode{0x201D}$.
A cylinder whose axis is not at $90^\circ$ to the circular faces is called an $\unicode{0x201C}Oblique\ Cylinder\unicode{0x201D}$.
-----------book page break-----------
The perpendicular distance between the two circular faces of a cylinder is called the height of the cylinder, shown as $h$ in both the figures.
The distance of the two circular faces along the lateral surface is called the length of the cylinder, shown as $l$ in the figures.
In case of a right circular cylinder the lateral length is same as the height of the cylinder.
Now, let us look at the ways to calculate the volume and surface area of the cylinders.
The volume, $V$ of a cylinder (both right circular and oblique) is given by:
$V = \pi r^2 h$
The area of the circular faces, $S_c$ is given by:
$S_c = \pi r^2 + \pi r^2 = 2\pi r^2$
The area of the lateral surface, $S_L$ is given by:
$S_L = 2\pi r l$, where $l$ is the lateral length.
In case of right circular cylinder, since lateral length is equal to the height of the cylinder, the lateral surface area is given by:
$S_L = 2\pi r l = 2\pi r h$
The total surface area of a cylinder $S$ is given by:
$S = 2\pi r^2 + 2\pi rl$
-----------book page break-----------
$\underline{III.\ Cones\ \&\ Pyramids}$
Cones are three dimensional objects formed by a plane circular base and a lateral surface. The figure below shows two cones.
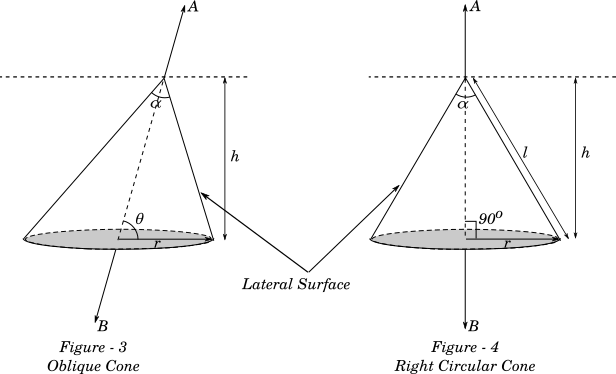
Each of the cones above have a line passing through the centre of the base and the apex of the cone. This line is called the axis of the cone. When the axis of the cone is perpendicular the the base, the cone is symmetrical around the axis, and this type of cones are called $\unicode{0x201C}Right\ Circular\ Cones\unicode{0x201D}$ and the cones whose axes are not perpendicular to the base are called $\unicode{0x201C}Oblique\ Cones\unicode{0x201D}$.
The distance between the apex of the cone and the plane of the base is called the height of the cone, as shown with $h$ in the above figures.
-----------book page break-----------
If a cone is cut by a plane passing through the axis, we get a triangle. The angle formed at the apex point of the triangle is called the $\unicode{0x201C}apex\ angle\unicode{0x201D}$. For a right circular cone the apex angle is constant, no matter at what angle the plane is drawn, while for an oblique cone, the apex angle depends on the angle at which the plane is drawn.
In the above figure $\alpha$ shows the apex angle.
The distance between the apex of the cone and any point on the circumference of the base along the lateral surface, is called the $\unicode{0x201C}Slant\ Height\unicode{0x201D}$ of the cone, indicated by $l$ in $Figure-4$.
As you may have observed, the slant height of the oblique cone is not constant, and varies with the point that you choose on the circumference of the base.
Now let's look at the ways to find out how to calculate the volume $V$ of a cone.
$V = \dfrac{1}{3} \pi r^2 h$
This is applicable for both oblique and right circular cones.
Also, note that the volume of any pyramid is given by:
$V = \dfrac{1}{3}\ (Area\ of\ base) \times height$
The lateral surface area $S_L$ of a right circular cone is given by:
$S_L = \pi r l$ where $l$ is the slant height of the cone.
If you know the height $h$ of the cone and the radius $r$, then the slant height can be obtained using:
$l = \sqrt{h^2 + r^2}$, and our formula for lateral surface area becomes:
$S_L = \pi r \times \sqrt{h^2 + r^2}$
Hence, the total area of a right circular cone is $\pi r \times \sqrt{h^2 + r^2} + \pi r^2$
-----------book page break-----------
It is quite easy and interesting to see why the lateral surface area of a right circular cone is $\pi r l$
Let's take a right circular cone with an open base, with the apex as point $A$, a slant height of $l$ and base radius $r$.
If we cut the cone along any of the slant heights and open the cone, we will get a sector as shown below. The apex $A$ of the cone will be the centre of this sector.

The radius of the sector will be $l$, which was the slant height of the cone, and the arc length of the sector will be $2\pi r$ which was the circumference of the base of the cone.
If we are able to calculate the area of the sector, that will give us the lateral surface area of the cone.
The complete circumference of the circle is $2 \pi l$
We can calculate the angle of the sector $\theta$ using the following steps:
The angle formed by the circumference $(2 \pi l)$ is $360^\circ$
-----------book page break-----------
The angle formed by an arc of length $1$ unit is $\left(\dfrac{360}{2 \pi l}\right)^\circ$
The angle formed by an arc of length $2 \pi r$ is $2 \pi r \times \dfrac{360}{2 \pi l} = \left(\dfrac{r \times 360}{l}\right)^\circ$
The area of the complete circle of radius $l$ is $\pi l^2$
The area of a sector whose angle is $1^\circ$ is $\dfrac{\pi l^2}{360}$
Therefore, the area of the sector, whose angle is $\left(\dfrac{r \times 360}{l}\right)^\circ$ is $\dfrac{r \times 360}{l} \times \dfrac{\pi l^2}{360} = \pi r l$
The $pyramid$ is a more general case of a $cone$ where the base can be of any regular or irregular polygon.
The pyramid is obtained by forming a triangle with each side of the base as its side, and the $apex$ as the opposite vertex of the triangle.
-----------book page break-----------
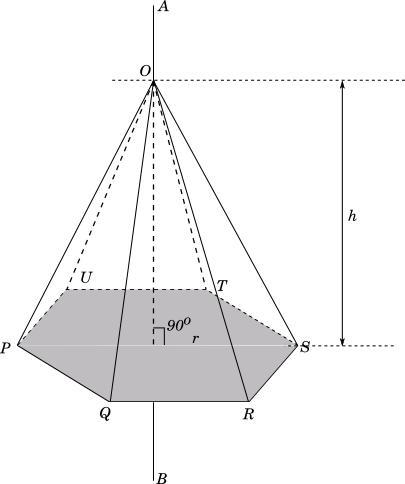
The figure below shows a pyramid with $O$ as the apex, and $PQRSTU$ as its $hexagonal$ base. The six lateral faces of this pyramid are $\triangle PQO$, $\triangle QRO$, $\triangle RSO$, $\triangle STO$, $\triangle TUO$ and $\triangle UPO$
-----------book page break-----------
The volume of the pyramid is $\dfrac{1}{3} \times (Area\ of\ PQRSTU) \times h$
Note that, there is no well known formula for calculating the lateral surface area of an oblique cone.