Menelaus's Theorem

$\underline{Theorem}:$

Given $\triangle ABC$ and a line $l$, not passing through any of the vertices, that intersects the two sides $AB, AC$ of the triangle internally and the third side $BC$ externally, at points $D, E$ and $F$ respectively, then the following relationship holds:

$\Rightarrow \dfrac{AD \cdot EC \cdot BF}{DB \cdot AE \cdot CF} = 1$

$\underline{Construction}:$

Draw $\triangle ABC$ with line $l$ intersecting $AB$ at $D$, $AC$ at $E$ and $BC$ extended at $E$.

Select any random point $P$ on the line segment $DE$, join $AP$.

Draw line $BQ \parallel AP$ intersecting line $l$ at $Q$ and $CR \parallel AP$ intersecting $l$ at $R$ as shown in the figure below.

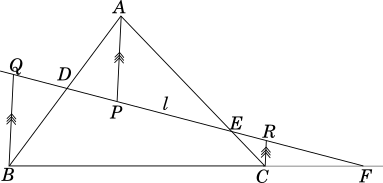
$\underline{Proof}:$

Since $BQ \parallel AP$, $\angle DBQ = \angle DAP$ and $\angle DQB = \angle DPA$

$\therefore \triangle BQD \sim \triangle APD$

-----------book page break-----------

Using properties of similar triangles, as explained ,

$\dfrac{AD}{DB} = \dfrac{AP}{BQ}$ $...eqn(i)$

Similarly,

$\triangle APE \sim \triangle CRE$

$\therefore \dfrac{EC}{AE} = \dfrac{CR}{AP}$ $...eqn(ii)$

and

$\triangle CFR \sim BFQ$

$\therefore \dfrac{BF}{CF} = \dfrac{BQ}{CR}$ $...eqn(iii)$

$eqn(i) \times eqn(ii) \times eqn(iii)$ gives us:

$\dfrac{AD}{DB} \times \dfrac{EC}{AE} \times \dfrac{BF}{CF} = \dfrac{AP}{BQ} \times \dfrac{CR}{AP} \times \dfrac{BQ}{CR}$

$\Rightarrow \dfrac{AD \cdot EC \cdot BF}{DB \cdot AE \cdot CF} = 1$