Angles In Alternate Segment

$\underline{Introduction:}$

For a straight line $AB$ tangent to a circle at $T$, and a chord $ST$, the angle in the alternate segment is defined as the angle subtended by $ST$ at any point $P$ such that $P$ is on the opposite side of $\angle STA$, the $\angle SPT$ is called the angle in the alternate segment of $\angle STA$

$\underline{Theorem:}$

For any circle, and a line $AB$ tangent to the circle at point $T$, the angle in alternate segment $\angle SPT = \angle STA$

-----------book page break-----------

$\underline{Construction:}$

A circle is drawn with $AB$ as tangent to it at $T$. Any random point $P$ is chosen on the segment opposite to the line $AT$ and lines $PS$ and $PT$ are joined. Points $S$ and $T$ are joined with the centre $O$ of the circle.

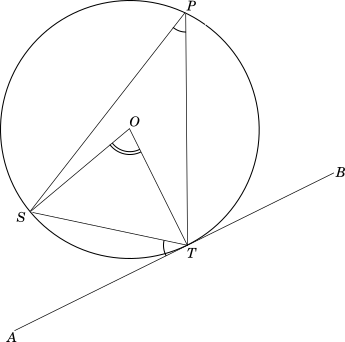
-----------book page break-----------

$\underline{Proof:}$

Considering $\triangle OST$

$OS = OT$, therefore $\triangle OST$ is isosceles with $\angle OST = \angle OTS$

Let's say $\angle OTS = x^\circ$

Therefore,

$x = \dfrac{180^\circ - \angle SOT}{2}$

$= 90^\circ - \dfrac{\angle SOT}{2}$

From this , we know that angle subtended by an arc at the centre is twice the angle subtended by the arc at the circumference.

Therefore, $\dfrac{\angle SOT}{2} = \angle SPT$

$\therefore x = 90^\circ - \angle SPT$

$\Rightarrow \angle SPT = 90 - x$

Since $AB$ is tangent at $T$ and $OT$ is the radius, $\angle OTA = 90^\circ$

Therefore,

$\angle STA + x^\circ = 90^\circ$

$\Rightarrow \angle STA = 90 - x$

Therefore,

$\angle STA = \angle SPT$