Area Of Triangle
I. Introduction
Here we are going to learn how to calculate the area of a triangle given the length of its base and the corresponding altitude. Let's begin by understanding what we mean by corresponding altitude.
If we take any triangle we can choose any one of the three sides as the base. If we draw a perpendicular to the base, or the extended base, from the opposite vertex, that is called the altitude or height corresponding to the selected base. Take a look at the triangles below.
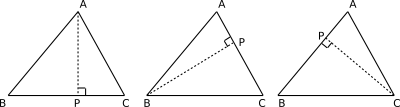
If you choose $BC$ as the base, then you need to draw a perpendicular from the vertex $A$ to $BC$ intersecting $BC$ at some point $P$. The line $AP$ is the altitude corresponding to the base $BC$. Similarly, if you choose $AC$ as the base, then $BP$ is the altitude, and if you choose $AB$ as your base, then $CP$ is the altitude.
What did we mean when we said drop a perpendicular to the extended base?
-----------book page break-----------
Look at the diagrams below:
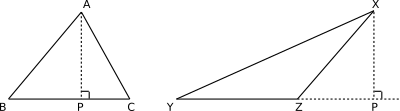
$\triangle ABC$ is an acute angle triangle with all angles less than $90^\circ$. If you choose any side as the base then the altitude will lie inside the triangle, intersecting the base internally. Now, let us look at $\triangle XYZ$ above, it is an obtuse angled triangle with $\angle XZY \gt 90^\circ$. In this case if you choose any one of the smaller sides, $YZ$ or $XZ$ as the base, the altitude will be outside the triangle and it will intersect the base, extended. In the above figure we chose $YZ$ as the base and we have $XP$ as the height.
-----------book page break-----------
Try the following widget. Click on any of the three sides or the three perpendiculars to see how the area remains same no matter which side you choose. You can also change the size (area) of the triangle by dragging the blue diamond or just slide the red dot to keep the area constant but still change the shape of the triangle.
-----------book page break-----------
II. Derivation
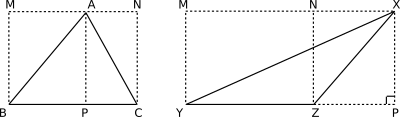
We have two figures above. The first one is an acute angled $\triangle ABC$, where the perpendicular $AP$ intersects the base $BC$ internally. The second one is an obtuse angled $\triangle XYZ$, with the perpendicular $XP$ intersecting the extended base $YZ$ externally. We will see the derivation of the formula for the area for both these cases.
$\underline{For\ \triangle ABC}$
We draw a line $MN$ parallel to the base $BC$ and draw perpendiculars from $B$ and $C$ on the line $MN$. We have two rectangles $MBPA$ and $ANCP$, with $AB$ and $AC$ as diagonals respectively. We know that the diagonal of a rectangle divides it into two identical triangles of equal area.
So $Area\ of\ \triangle ABP = \dfrac{1}{2} \times (Area\ of\ MBPA)$,
$= \dfrac{1}{2} \times BP \times AP$
Similarly, $Area\ of\ \triangle ACP = \dfrac{1}{2} \times (Area\ of\ ANCP)$
$= \dfrac{1}{2} \times PC \times AP$
$Area\ of\ \triangle ABC = Area\ of\ \triangle ABP + Area\ of\ \triangle ACP$
$\texttip{\therefore}{therefore}\ Area\ of\ \triangle ABC$
$= \dfrac{1}{2} \times AP \times BP + \dfrac{1}{2} \times AP \times PC$
$= \dfrac{1}{2} \times AP \times (BP + PC)$
But, $BP + PC = BC$
$\texttip{\therefore}{therefore} Area\ of\ \triangle ABC = \dfrac{1}{2} \times AP \times BC = \dfrac{1}{2} \times base \times height$
$\underline{For\ \triangle XYZ}$
Let us draw lines $XM$ parallel to $PY$, $YM$ and $ZN$ parallel to $PX$, such that $XMPY$ and $XNZP$ are rectangles with $XY$ and $XZ$ as a diagonals respectively.
-----------book page break-----------
$Area\ of\ \triangle XYP = \dfrac{1}{2} \times (area\ of\ XMPY)$
$= \dfrac{1}{2} \times PY \times XP$
$Area\ of\ \triangle XZP = \dfrac{1}{2} \times (area\ of\ XNZP)$
$= \dfrac{1}{2} \times ZP \times XP$
As we can see,
$Area\ of\ \triangle XYZ = (Area\ of\ XYP) - (Area\ of\ XZP)$
$\texttip{\therefore}{therefore} Area\ of\ \triangle XYZ$
$= \dfrac{1}{2} \times PY \times XP - \dfrac{1}{2} \times ZP \times XP$
$= \dfrac{1}{2} \times XP \times (PY - ZP)$
$= \dfrac{1}{2} \times XP \times YZ$
$= \dfrac{1}{2} \times base \times height$
So, we see that the area of a triangle can be calculated by taking any one of the sides as base and drawing a perpendicular from the opposite vertex to the base or the extended base, and finding half the product of the base and the height.
Concept Of Area -