Area Of Quadrilaterals

In case of a parallelogram, the area can be calculated using:

$Area = \dfrac{1}{2}\times (length\ of\ a\ side) \times (height)$

Let's consider the parallelograms $ABCD$ shown below:

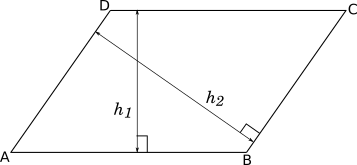
We know that in a parallelogram opposite sides are equal.

$\texttip{\therefore}{therefore} AB = DC$ and $BC = AD$.

The height of a parallelogram can be the distance between any two pairs of parallel lines.

If we chose $AB$ or $CD$ as our side, then the height should be $h_1$, whereas, if we choose $BC$ or $AD$ as our side then the height should be $h_2$.

Hence,

$Area\ of\ \unicode{0x25B1} ABCD = AB \times h_1 = CD \times h_1 = BC \times h_2 = AD \times h_2$

-----------book page break-----------

II. Area Of Trapezium

The area of a trapezium can be calculated using:

$Area = (\text{Average length of the two parallel sides})$

$\times (\text{distance between the two parallel sides})$

Let us consider the trapezium $PQRS$ with $PQ \parallel SR$, as shown below.

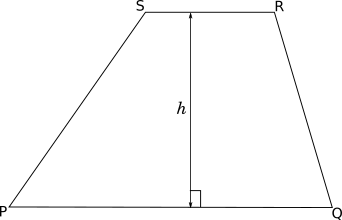
Since a trapezium has only one pair of parallel lines, it can have only one height, which is the distance between the two parallel lines.

The area of $PQRS$ is:

$h \times \dfrac{PQ + RS}{2}$

-----------book page break-----------

III. Area Of Kite

The area of a kite can be calculated easily if the two diagonals are known, using:

$Area = \dfrac{1}{2} \times (\text{Length of the first diagonal})$

$\times (\text{Length of the second diagonal})$

Let us look at the quadrilateral $ABCD$, which is a kite.

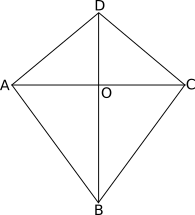
In a kite the diagonals intersect each other at $90^\circ$.

Consider $\triangle ACD$, with $AC$ as the base and $DO$ as the altitude.

Hence area of $\triangle ACD = \dfrac{1}{2} \times AC \times DO$

Similarly, in $\triangle ACB$, if we take $AC$ as the base, and $BO$ as the altitude.

Hence, area of $\triangle ABC = \dfrac{1}{2} \times AC \times BO$

-----------book page break-----------

Therefore, area of $ABCD = \dfrac{1}{2} \times AC \times DO + \dfrac{1}{2} \times AC \times BO$

$= \dfrac{1}{2} \times AC \times (DO + BO)$

$= \dfrac{1}{2} \times AC \times BD$

Note that, since squares and rhombuses are also kites, that is, their diagonals intersect each other at $90^\circ$, you can use this method to calculate the area of squares and rhombuses when the diagonal lengths are known.