Areas Formed By Lines Parallel To The Sides Passing Through A Point In A Triangle

$\underline{Theorem}$

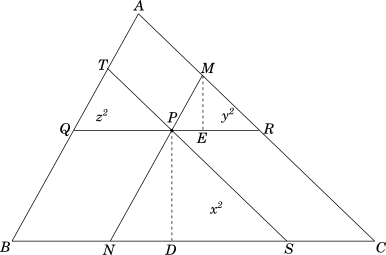
Let us consider a triangle $ABC$ and an internal point $P$. Lines $MN$, $QR$ and $ST$ are drawn through $P$ inside $\triangle ABC$, parallel to $AB$, $BC$ and $CA$ respectively, each terminated by the other two sides of the triangle.

If $ar[\triangle PNS]$, $ar[\triangle PTQ]$ and $ar[\triangle PRM]$ are $x^2$, $y^2$ and $z^2$ respectively then the $ar[\triangle ABC] = (x + y + z)^2$

$\underline{Construction}$

We will draw the altitudes $PD$ and $ME$ of $\triangle PNS$ and $\triangle MPR$ from vertices $P$ and $M$ to their opposite sides.

-----------book page break-----------

$\underline{Proof}$

Considering $\triangle PNS$ and $\triangle ABC$,

$\angle PNS = \angle ABC$ $\because PN \parallel AB$

$\angle PSN = \angle ACB$ $\because TS \parallel AC$

Therefore the third angles $\angle BAC = \angle NPS$

$\therefore \triangle PNS \sim \triangle ABC$

Similarly, we can show that $\triangle TQP \sim \triangle ABC$ and $\triangle MPR \sim \triangle ABC$

Since all the three triangle are similar to $\triangle ABC$ they are similar to each other.

Considering $\triangle s\ PMS$ and $MPR$

$\dfrac{ar[\triangle PNS]}{ar[\triangle MPR]} = \dfrac{x^2}{y^2} = \dfrac{NS^2}{PR^2}$

$\Rightarrow \dfrac{x}{y} = \dfrac{NS}{PR}$ Let;s say $= k$

Since the sides and other dimensions of $\triangle PNS$ and $\triangle MPR$, we can write:

$\dfrac{NS}{PR} = \dfrac{PS}{MR} = \dfrac{PD}{ME} = \dfrac{x}{y}$

Let $NS = k_1 \times x$

$PR = k_1 \times y$

And $PD = k_2 \times x$

$ME = k_2 \times y$

Because $PR \parallel SC$ and $PS \parallel RC$, $PSCR$ is a parallelogram.

$ar[PSCR] = SC \times PD = PR \times PD = k_1 \times y \times k_2 \times x$

$ar[\triangle PNS] = \dfrac{1}{2} \times NS \times PD = \dfrac{1}{2} k_1 \times x \times k_2 \times x$

Therefore,

$\dfrac{ar[PSCR]}{ar[\triangle PNS]} = \dfrac{k_1 \times y \times k_2 \times x}{\frac{1}{2} k_1 \times x \times k_2 \times x} = \dfrac{2y}{x}$

-----------book page break-----------

Since the $ar[\triangle PNS]$ is given as $x^2$, we get:

$\dfrac{ar[PSCR]}{x^2} = \dfrac{2y}{x}$

$\Rightarrow ar[PSCR] = 2xy$

Similarly, we can show that:

$ar[PMAT] = 2yz$ and $ar[PNBQ] = 2zx$

$ar[\triangle ABC] = x^2 + y^2 + z^2 + 2xy + 2yz + 2zx = (x + y + z)^2$

Note the following few observations from this proof:

$ar[\triangle AQR] = y^2 + z^2 + 2yz = (y + z)^2$

Similarly

$ar[\triangle BST] = z^2 + x^2 + 2zx = (z + x)^2$

$ar[\triangle CMN] = x^2 + y^2 + 2xy = (x + y)^2$