Perpendicular Bisectors & Circumcentre Of Triangles

In this topic we will learn about the properties of the perpendicular bisectors of the sides of a triangle and the circumcentre.

First we will see that the perpendicular bisectors of the three sides of a triangle are concurrent, that is they pass through the same point, then we will learn a few properties of this point.

$\underline{Theory}$

The perpendicular bisectors of the three sides of any triangle passes through a common intersection point.

$\underline{Construction}$

Let us draw a triangle $ABC$. Let $OR$ be the perpendicular bisector of $AB$, and $OQ$ be the perpendicular bisector of $AC$ and they meet at $O$. Let us draw a line $OP$ perpendicular to $BC$ at point $P$.

If we can show that $P$ is the midpoint of $BC$ then that would mean that $OP$ is the perpendicular bisector of $BC$ and since it passes through $O$, it would prove that the perpendicular bisectors of the sides of a triangle are concurrent.

Let us join the three vertices $A$, $B$ and $C$ with the point $O$ as shown in the following diagram in blue.

-----------book page break-----------

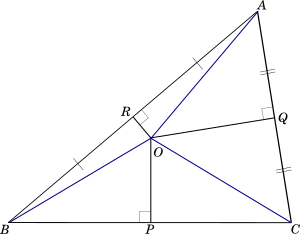
$\underline{Proof:}$

In $\triangle$s $QOC$ and $QOA$

$QC = QA$ $\texttip{\because}{because}$ $Q$ is the midpoint of $AC$

$\angle CQO = \angle AQO$ $\texttip{\because}{because}$ $OQ \perp AC$ both are $90^\circ$

$OQ$ is common.

$\texttip{\therefore}{therefore} \triangle QOC \texttip{\cong}{congruent to} \triangle QOA$

$\texttip{\Rightarrow}{follows that} OC = OA$

Similarly, in $\triangle$s $ROA$ and $ROB$

$RA = RB$ $\texttip{\because}{because}$ $R$ is the midpoint of $AB$

$\angle ARO = \angle BRO$ $\texttip{\because}{because}$ $OR \perp AB$ both are $90^\circ$

$OR$ is common.

$\texttip{\therefore}{therefore} \triangle ROA \texttip{\cong}{congruent to} \triangle ROB$

$\texttip{\Rightarrow}{follows that} OA = OB$

-----------book page break-----------

$\texttip{\because}{because} OC = OA$ and $OA = OB$ $\texttip{\Rightarrow}{follows that} OC = OB$

Now, considering $\triangle$s $OPB$ and $OPC$, we have:

$\angle OPB = \angle OPC = 90^\circ$ $\texttip{\because}{because}$ $OP \perp BC$

$OC = OB$

$OP$ is common.

$\texttip{\therefore}{therefore}$ using the $RHS$ rule, $\triangle OPB \texttip{\cong}{congruent to} \triangle OPC$

$\texttip{\therefore}{therefore} PB = PC \texttip{\Rightarrow}{follows that} P$ is the midpoint of $BC$

Therefore, the perpendicular bisectors of the three sides of a triangle are concurrent.

We have seen that this point is equidistant from the three vertices, that is, $OA = OB = OC$.

Therefore, if we draw a circle with $O$ as the centre and $OA$ as the radius, it will pass through all the three vertices of the triangle, as shown in the following figure:

-----------book page break-----------

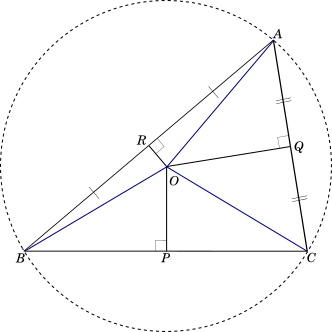
$\underline{Definitions:}$

$\bullet$ The circle shown above, passing through all the vertices of the triangle is called the $\unicode{0x201C}Circumcircle\unicode{0x201D}$

$\bullet$ The centre of the circumcircle, which is the intersection point of the perpendicular bisector of the sides is called the $\unicode{0x201C}Circumcentre\unicode{0x201D}$

$\bullet$ The distance from the circumcentre to any of the vertices is called the $\unicode{0x201C}Circumradius\unicode{0x201D}$

-----------book page break-----------

$\underline{Properties\ of\ Circumcentre}$

$\bullet$ In an acute angled triangle the circumcentre lies inside the triangle.

$\bullet$ In a right angled triangle the circumcentre is the midpoint of the hypotenuse.

This means that the median, which joins the $90^\circ$ vertex to the midpoint of the hypotenuse, is equal to half the hypotenuse.

$\bullet$ In an obtuse angled triangle the circumcentre lies outside the triangle.