Types Of Triangles And Their Properties

General Properties Of Triangles
Sum of any two sides of a triangle is greater than the $3\xasuper{rd}$ side.

     

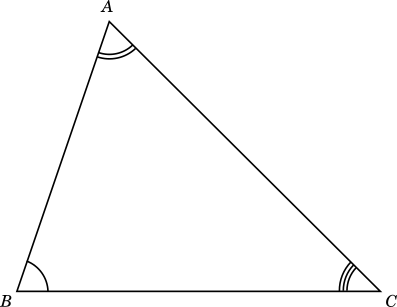
In the above figure, if we take any two sides of $\triangle ABC$, then their sum would be greater than the third side.
Thus,

$AB + BC \gt CA$
$BC + CA \gt AB$, and
$CA + AB \gt BC$

-----------book page break-----------
Sum of the $3$ angles is always $180^\circ$
In $\triangle ABC$ shown above, the marked angles sum up to $180^\circ$, that is,
$\angle ABC  + \angle BCA + \angle CAB = 180^\circ$

Scalene Triangle
If the triangle has no two sides equal to each other, all of its angles are also different. A triangle having all three sides of different length and all angles of different magnitude is called a scalene triangle.
The angle opposite to the largest side is of the largest magnitude and the angle opposite to the smallest side has the smallest magnitude.

-----------book page break-----------
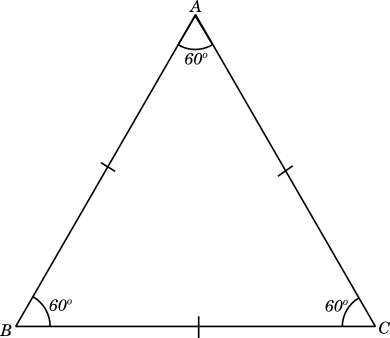
Equilateral Triangle
All three sides of an equilateral triangle are equal, so are the $3$ angles, each being equal to $180 \div 3 = 60^\circ$
The figure below shows an equilateral triangle.
     


-----------book page break-----------
Isosceles Triangle
Any two sides of the triangle are equal.
The angles opposite to the equal sides are equal.
The figure below shows an isosceles triangle $ABC$ with $AB = AC$

     

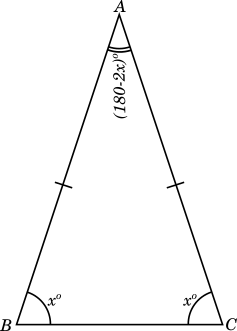
The angle opposite to $AB$ is $\angle ACB$ and the angle opposite to $AC$ is $\angle ABC$, and
$\angle ACB = \angle ABC$.
If each one of them is $x^\circ$, then,
$\angle BAC = 180 - (x + x) = (180 - 2x)^\circ$


-----------book page break-----------
Acute Angled Triangle
All the angles of an acute angled triangle are less than $90^\circ$

Right Angled Triangle
One of the angles of the triangle is equal to $90^\circ$
The figure below shows $\triangle ABC$ which has $\angle ABC = 90^\circ$.
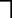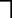A $90^\circ$ angle is normally shown using the    symbol, as shown in the figure for $\angle ABC$.

     

In a right angled triangle, there can be only one angle equal to $90^\circ$, the other two must be less than $90^\circ$ each, otherwise, their sum would exceed $180^\circ$.

-----------book page break-----------
You can also observe that since one angle is $90^\circ$, the sum of the other two should be $180 - 90 = 90^\circ$
In our figure,
$\angle BAC + \angle ACB = 90^\circ$

Obtuse Angled Triangle
When any one of the angles of a triangle exceeds $90^\circ$, the triangle is called obtuse angled triangle.
In the figure below $\triangle ABC$ has $\angle A = 110^\circ$, $\angle B = 40^\circ$ and $\angle C = 30^\circ$

     

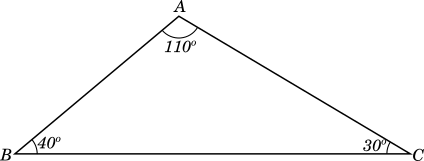
Since $\angle A$ exceeds $90^\circ$ it is an obtuse angled triangle.
It is evident, that the other two angles of an obtuse angle triangle $MUST\ BE$ less than $90^\circ$, otherwise their sum would exceed $180^\circ$