Medians & Centroid Of Triangles
Today we will see some properties of the medians of triangles.
$\underline{Theorem:}$
The three medians of a triangle are concurrent, that is, they pass through a single point.
Let us say we have any triangle $ABC$ with $Q$ as the midpoint of $AC$ and $R$ as the midpoint of $AB$.
$BQ$ and $CR$ are the two medians of $\triangle ABC$. Let's say they intersect at point $G$.
We can join points $A$ and $G$ with a straight line and extend that line to meet side $BC$ at point $P$. If we can show that $P$ is the midpoint of $BC$ then we have shown that the medians of a triangle are concurrent.
-----------book page break-----------
$\underline{Construction:}$
Let us extend line $AP$ to $E$ such that $GE = AG$. Draw lines $BE$ and $CE$. We should get the diagram below:
We should get a figure similar to the one below (constructions are shown in blue).
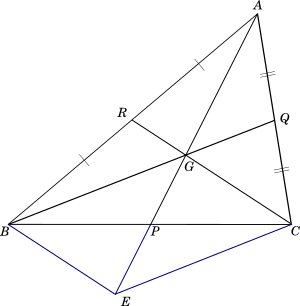
$\underline{Proof:}$
Let us consider $\triangle ABE$.
$AR = BR$ $\texttip{\because}{because}$ $R$ is the midpoint of $AB$
$AG = GE$ by construction.
$\texttip{\therefore}{therefore} RG \parallel BE$
$\texttip{\therefore}{therefore} GC \parallel BE$ $\texttip{\because}{because}$ $RG$ and $GC$ are the same straight lines.
-----------book page break-----------
Similarly considering $\triangle ACE$
$AQ = CQ$ $\texttip{\because}{because}$ $Q$ is the midpoint of $AC$
$AG = GE$ by construction.
$\texttip{\therefore}{therefore} GQ \parallel CE$
$\texttip{\therefore}{therefore} BG \parallel CE$ $\texttip{\because}{because}$ $BG$ and $GQ$ are the same straight lines.
Therefore, the quadrilateral $BGCE$ is a parallelogram, since opposite sides are parallel.
We know that the diagonals of a parallelogram bisect each other, hence $P$ is the midpoint of $BC$ and $GE$.
Since $P$ is the midpoint of $BC$, $AP$ is the median.
$\underline{Definition - 1:}$
The intersection point of the medians of a triangle is called the $\unicode{0x201C}centroid\unicode{0x201D}$ of the triangle.
$\underline{Corollary-1:}$
The centroid divides the median in the ratio $2:1$
In the above diagram:
$GE = AG$ and $GP = \dfrac{1}{2} GE$
$\texttip{\therefore}{therefore} GP = \dfrac{1}{2} GE$
$\texttip{\Rightarrow}{follows that} GE:GP = 2:1$
$\underline{Corollary-2:}$
The centroid, when joined to the $3$ vertices of a triangle, we get $3$ triangles of equal area.
In the above diagram $\texttip{[\triangle GAB]}{area of} = \texttip{[\triangle GBC]}{area of} = \texttip{[\triangle GCA]}{area of} = \dfrac{1}{3}\texttip{[\triangle ABC]}{area of}$
-----------book page break-----------
To prove this we can extend our diagram by drawing perpendiculars from $G$ and $A$ to the line $BC$ as shown in the following diagram.
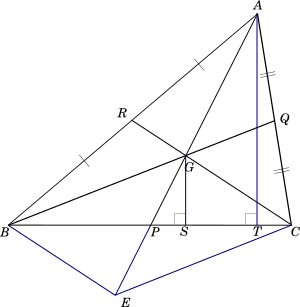
$\underline{Proof:}$
$GS \parallel AT$ $\texttip{\because}{because}$ $GS$ and $AT$ are perpendiculars to the same line $BC$.
$\texttip{\therefore}{therefore} \triangle PSG \texttip{\sim}{similar to} \triangle PTA$
$\texttip{\Rightarrow}{follows that} \dfrac{GP}{AP} = \dfrac{GS}{AT} = \dfrac{PS}{PT}$
We know from Corollary-1 that $GP:GA = 1:2$
-----------book page break-----------
$\texttip{\therefore}{therefore} \dfrac{GP}{AP} = \dfrac{1}{3}$
$\texttip{\Rightarrow}{follows that} \dfrac{GS}{AT} = \dfrac{1}{3} \texttip{\Rightarrow}{follows that} GS = \dfrac{1}{3} \times AT$
$\texttip{[\triangle ABC]}{area of} = \dfrac{1}{2} \times AT \times BC$
$\texttip{[\triangle GBC]}{area of} = \dfrac{1}{2} \times GS \times BC$
$= \dfrac{1}{2} \times \left(\dfrac{1}{3} \times AT \right) \times BC$
$= \dfrac{1}{3} \times \left(\dfrac{1}{2} \times AT \times BC \right)$
$= \dfrac{1}{3} \times \texttip{[\triangle ABC]}{area of}$
Similarly for each of the other two $\triangle$s $GAB$ and $GAC$ we can prove that:
$\texttip{[\triangle GAB]}{area of} = \dfrac{1}{3} \times \texttip{[\triangle ABC]}{area of}$
$\texttip{[\triangle GCA]}{area of} = \dfrac{1}{3} \times \texttip{[\triangle ABC]}{area of}$
$\texttip{\therefore}{therefore} \texttip{[\triangle GAB]}{area of} = \texttip{[\triangle GBC]}{area of} = \texttip{[\triangle GCA]}{area of} = \dfrac{1}{3} \times \texttip{[\triangle ABC]}{area of}$