Continuity Of Functions
I. Introduction:
The concept of continuity of a function draws heavily from the concept of limits covered .
Given a function $f$ of $x$, $f(x)$ is said to be continuous at $x = a$ if, both left and right side limits of $f(x)$ as $x \rightarrow a$ exist, and
$\lim\limits_{x \rightarrow a-} f(x) =$
$\lim\limits_{x \rightarrow a+} f(x)$
$=$ $f(a)$
II. Types Of Discontinuity
If for function $f(x)$, and a given value $a$
$\lim\limits_{x \rightarrow a-} f(x) = \lim\limits_{x \rightarrow a+} f(x) \ne f(a)$ then $a$ is called a removable discontinuity.
If, on the other hand,
$\lim\limits_{x \rightarrow a-} f(x) \ne \lim\limits_{x \rightarrow a+} f(x)$, then $a$ is a non-removable discontinuity, and the difference:
$\left\lvert \lim\limits_{x \rightarrow a+} f(x) - \lim\limits_{x \rightarrow a-} f(x) \right\rvert$ is called the jump of $f(x)$ at $x = a$.
Before we move on to the next sections to understand various types of discontinuities, let us try the following problem:
-----------book page break-----------
--------- Reference to question: ddf2a044-1e1f-453e-a51d-4a80cb8c0ebf ---------
Now let us move on to the next sections to understand the different types of discontinuities.
-----------book page break-----------
III. Removable Discontinuities
There are two types of discontinuities which can be ignored and the function can be treated as continuous at the point of concern. These are called removable discontinuities, and are of the following types:
Missing Point Discontinuity
If a function $f(x)$ is defined such that $\lim\limits_{x \rightarrow a-} f(x) = \lim\limits_{x \rightarrow a+} f(x)$, but $f(a)$ is not defined then it is called a missing point discontinuity.
However, these types of discontinuities can be ignored for all practical purposes, because, we can bring $x$ arbitrarily close to the value $a$ and get a valid value of the function.
The following is an example of missing point discontinuity.
$f(x) = \dfrac{x^2 + x - 12}{x - 3}$
Factorising the numerator, we can write the above function as:
$f(x) = \dfrac{(x + 4)(x - 3)}{x - 3}$
At $x = 3$ the function becomes undefined, since the function takes the indeterminate form
$\dfrac{0}{0}$
Isolated Point Discontinuity
Let's take a look at the following function:
$f(x) = \left\{\begin{array}{ll} x + 5 & \text{for } x \ne 3 \\ 9 & \text{for } x = 3 \end{array} \right.$
-----------book page break-----------
If we plot this function, we get the following graph:
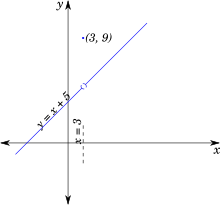
We can see that the function has a discontinuity at $x = 3$, because:
$\lim\limits_{x \rightarrow 3-} f(x) = \lim\limits_{x \rightarrow 3+} f(x) =$
$8$
Also, $f(3)$ is defined, and is equal to $9$.
Therefore,
$\lim\limits_{x \rightarrow 3-} f(x) = \lim\limits_{x \rightarrow 3+} f(x) \ne f(3)$
Similar to the missing point discontinuity, we can make $x$ arbitrarily close to $3$, without actually being $3$, and get an almost continuous function.
A good way to think about either of the above types of discontinuities is that, the discontinuity occurs at a point, while the values immediately before and after converge to the same value.
-----------book page break-----------
Since a point is dimensionless, that is, it does not have any width, we can say that the discontinuity is dimensionless, that is it is a zero length discontinuity, and since the immediate left and right values converge, the point of discontinuity can be ignored and we can treat these as continuous functions.
IV. Non-Removable Discontinuity
There are certain types of discontinuity that cannot be removed.
These are as follows:
Jump Discontinuity
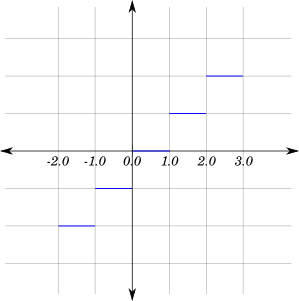
Let us consider the function $f(x) = \lfloor x \rfloor$, that is, $f(x)$ is the greatest integer $\le x$. The plot of this function will be as follows:
-----------book page break-----------
Now, we can see, that there is a clear discontinuity at all $x = n$ where $n \in \mathbb{Z}$. Let us take the example of $n = 2$
$\lim\limits_{x \rightarrow 2-} f(x)= 1$ whereas
$\lim\limits_{x \rightarrow 2+} f(x) = 2$ and
$f(2) = 2$
Therefore,
$\lim\limits_{x \rightarrow 2-} f(x) \ne \lim\limits_{x \rightarrow 2+} f(x) = f(2)$
In this case, there is a jump between the left hand and right hand limits, and is not a point difference and has a magnitude, therefore it is not possible to ignore the discontinuity, hence making it a non-removable discontinuity.
Infinite Type Discontinuity
If for a function $f(x)$, there is a point $x = a$, where
$\lim\limits_{x \rightarrow a-} f(x) = \pm \infty$ and/or $\lim\limits_{x \rightarrow a+} f(x) = \pm \infty$ then the discontinuity is non-removable, and is called Infinite type discontinuity.
Let us take the example of the function:
$f(x) = \dfrac{1}{x - 5}$
Therefore,
$\displaystyle \lim\limits_{x \rightarrow 5^{-}} \dfrac{1}{x - 5} = -\infty$
and
$\displaystyle \lim\limits_{x \rightarrow 5^{+}} \dfrac{1}{x - 5} = +\infty$
Therefore, the function is discontinuous at $x = 5$ and the discontinuity cannot be removed.
-----------book page break-----------
Oscillatory Discontinuity
These discontinuities are seen in functions of the form $f(g(x))$, where $f$ is an oscillatory function, like any of the trigonometric function, and $g$ is not defined at $x = a$. We can take the example where $f(x) = \sin x$ and $g(x) = \dfrac{2\pi}{x - 3}$
Therefore,
$f(g(x)) = \sin \left( \dfrac{2\pi}{x - 3}\right)$
We can see that as $x$ approaches $3$ from either side, $\dfrac{2\pi}{x - 3}$ grows to infinity.
Let us see what happens when $x$ decreases from $4$ to $3$.
At $x = 4$, $g(x) = 2\pi$, and at $x = 3.5$, $g(x) = 4\pi$. Therefore between $x = 4$ and $3.5$, $f(g(x))$ will have one complete oscillation.
Now let us see some more values for which $g(x)$ is equal to some multiple of $2 \pi$, that is, $2n\pi$, where $n \in \mathbb{Z}$.
At $x = 3\dfrac{1}{3}$, $g(x) = 2 \cdot 3 \cdot \pi$.
Similarly, if we continue further, we will get the following table:
| $x$ | $n$ | $z = \dfrac{2\pi}{x - 3}$ | $\Delta x$ |
| $4$ | $1$ | $2 \cdot 1 \cdot \pi$ | - |
| $3\dfrac{1}{2}$ | $2$ | $2 \cdot 2 \cdot \pi$ | $\dfrac{1}{2}$ |
| $3\dfrac{1}{3}$ | $3$ | $2 \cdot 3 \cdot \pi$ | $\dfrac{1}{6}$ |
| $3\dfrac{1}{4}$ | $4$ | $2 \cdot 4 \cdot \pi$ | $\dfrac{1}{12}$ |
-----------book page break-----------
As we can see from the above table, the $\Delta x$ value for one complete oscillation of $f(g(x))$, is of the form:
$\dfrac{1}{n-1} - \dfrac{1}{n} = \dfrac{1}{(n-1)n}$
As $x$ approaches $3$, $n$ approaches $\infty$ and $\dfrac{1}{(n-1)n}$ approaches $0$, which means the curve oscillates infinitely fast as $x$ approaches $3$. The behaviour is same as $x$ approaches $3$ from the left side.
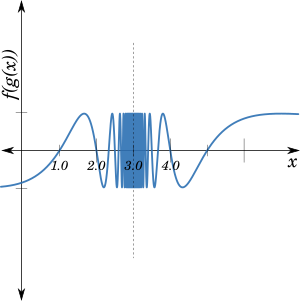
The following is the plot of the actual curve of $\sin \left(\dfrac{2 \pi}{x - 3}\right)$
-----------book page break-----------
Therefore, we can conclude that as $x$ approaches $3$ from either side, the value of $f(g(x))$ doesn't approach any particular value, instead oscillates infinitely fast.
Therefore, the jump of the function at $x = 3$ is undefined, making it impossible to remove this type of discontinuity.
V. Properties Of Continuity
If functions $f(x)$ and $g(x)$ are continuous at the point $x = a$, then the functions,
$f(x) \pm g(x)$, $f(x) \cdot g(x)$ are also continuous at $x = a$, while
$\dfrac{f(x)}{g(x)}$ is continuous if $g(a) \ne 0$
If $g(x)$ is continuous at $x = a$, and $\lim\limits_{x \rightarrow a} g(x) = L$, then $f \circ g$ is continuous, if $f(x)$ is continuous at $x = L$