Tangential Quadrilateral & Incircle

We know that every circle has an incircle. Today we are going to learn about incircles of quadrilaterals and polygons in general.

Not every quadrilateral can have an incircle, only some, with a some special properties can have an incircle. These quadrilaterals are called inscribable.

Pitot's theorem states that for a tangential quadrilateral, the sum of the opposite sides are equal, that is quadrilateral $ABCD$ can have an incircle if the sum of the opposite sides are equal.

$\underline{Theorem\ I}$

For a quadrilateral with an incircle, sum of the opposite sides are equal.

$\underline{Construction}$

Let us draw a quadrilateral $ABCD$ and its incircle $\Omega$. Let us mark the four tangential points as $P$, $Q$, $R$ and $S$ as shown in the diagram.

-----------book page break-----------

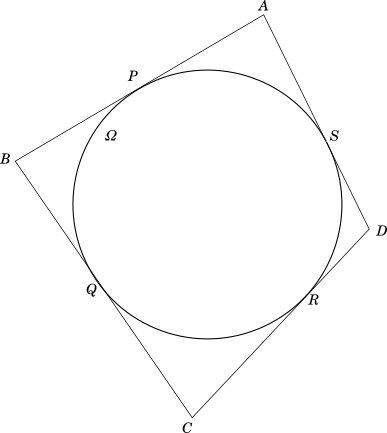
$\underline{Proof}$

Taking the pair of opposite sides $AB$ and $CD$, we can see that,

$AB + CD = AP + BP + CR + DR$ $...eqn\ (i)$

Since $AP$ and $AS$ are tangents to a circle from the same point $A$, $AP = AS$.

Similarly $BP = BQ$, $DR = DQ$ and $CR = CS$

-----------book page break-----------

Therefore, we can write $eqn\ (i)$ as:

$AB + CD = AP + BP + CR + DR$

$\Rightarrow AB + CD = AS + BQ + CS + DQ$

$\Rightarrow AB + CD = $AS + CS + BQ + DQ$

$\Rightarrow AB + CD = $AC + BD$

Now we will see how the length of the inradius of a tangential quadrilateral is related to its area and length of its sides.

We saw , that for any triangle $area = r \times \text{semi-perimeter}$, we will see here that the same relationship holds for a quadrilateral or any $n$-sided polygon that has an incircle.

$\underline{Theorem\ II}$

The area of a tangential quadrilateral $ABCD$ is given by:

$ar[ABCD] = r \times \text{semi-perimeter}$

$\underline{Construction}$

In the same diagram above, we join the points $A$, $B$, $C$, $D$ and $P$, $Q$, $R$, $S$ with the centre $O$ of the circle $\Omega$

-----------book page break-----------

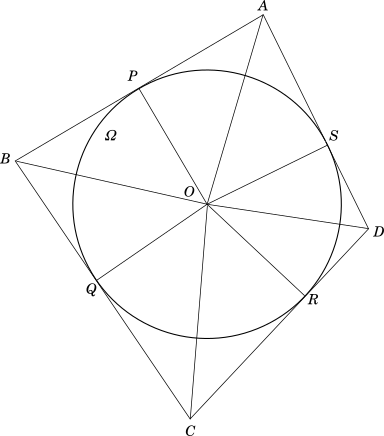
$\underline{Proof}$

Since $AB$, $BC$, $CD$ and $DA$ are tangents to the circle $\Omega$, $OP$, $OQ$, $OR$ and $OS$ are perpendiculars to these sides respectively.

$ar[\triangle OAB] = \dfrac{1}{2} \times OP \times AB = \dfrac{1}{2} \times r \times AB$

-----------book page break-----------

Similarly,

$ar[\triangle OBC] = \dfrac{1}{2} \times r \times BC$

$ar[\triangle OCD] = \dfrac{1}{2} \times r \times CD$

$ar[\triangle ODA] = \dfrac{1}{2} \times r \times DA$

$ar[ABCD] = ar[\triangle OAB] + ar[\triangle OBC] + ar[\triangle OCD] + ar[\triangle ODA]$

$= \dfrac{1}{2} \times r \times AB + \dfrac{1}{2} \times r \times BC + \dfrac{1}{2} \times r \times CD + \dfrac{1}{2} \times r \times DA$

$= \dfrac{1}{2} \times r \times (AB + BC + CD + DA)$

$= r \times \dfrac{AB + BC + CD + DA}{2}$

$= r \times \text{semi-perimeter}$

$\underline{Corollary\ 1:}$

The area of a tangential quadrilateral $ABCD$ is given by:

$ar[ABCD] = \sqrt{abcd} \times sin\dfrac{A + C}{2}$ where $a$, $b$, $c$, $d$ are the lengths of the four sides of $ABCD$ as marked in the diagram.

$\underline{Construction}$

We repeat the diagram from the first theorem, with the lengths of each side marked as $a$, $b$, $c$ and $d$ as shown below:

-----------book page break-----------

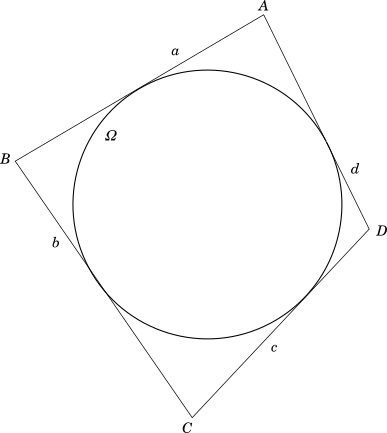
$\underline{Proof}$

Since, $ABCD$ is a convex quadrilateral, its area is given by:

$ar[ABCD] = \sqrt{(s - a)(s - b)(s - c)(s - d) - abcd.cos^2\left(\dfrac{A + C}{2}\right)}$

where $s$ is the semi-perimeter $= \dfrac{a + b + c + d}{2}$.

-----------book page break-----------

For a tangential quadrilateral we have, we can write

$s = \dfrac{a + b + c + d}{2} = \dfrac{2a + 2c}{2} = a + c$,

$\therefore s - a = c$

Similarly,

$s - b = d$

$s - c = a$

and

$s - d = b$

Therefore, we get:

$ar[ABCD] = \sqrt{abcd - abcd.cos^2\left(\dfrac{A + C}{2}\right)}$

$\Rightarrow ar[ABCD] = \sqrt{abcd\left\{1 - cos^2\left(\dfrac{A + C}{2}\right)\right\}}$

$\Rightarrow ar[ABCD] = \sqrt{abcd.sin^2\left(\dfrac{A + C}{2}\right)}$

$\Rightarrow ar[ABCD] = \sqrt{abcd}.sin\left(\dfrac{A + C}{2}\right)$

Observe, that the formula is applicable for the other pair of opposite angles as well, since:

$sin\left(\dfrac{B + D}{2}\right) = sin\left(\dfrac{360 - (A + C)}{2}\right)$

$= sin\left(180 - \dfrac{A + C}{2}\right) = sin\left(\dfrac{A + C}{2}\right)$

-----------book page break-----------

$\underline{Corollary\ 2:}$

The area of a tangential quadrilateral of given side lengths is maximum when the quadrilateral is cyclic, that is, it has a circumcircle.

These types of quadrilaterals which have both incircle and circumcircle are also called bicentric quadrilateral.

This corollary is a direct consequence of the previous corollary.

The are of the incircle is maximum when $sin\left(\dfrac{A + C}{2}\right) = 1$

Since $\dfrac{A + C}{2} \lt 360^\circ$, $\dfrac{A + C}{2} = 90^\circ$

$\therefore A + C = 180^\circ$,

and

$B + D = 360^\circ - (A + C) = 180^\circ$

Since the opposite angles sum up to $180^\circ$ this is a cyclic quadilateral.