Zeros Of A Polynomial

I. Introduction

If a polynomial $P(x)$ has a degree of $n$, that is, the polynomial is of the form $ax^n + bx^{n-1} + cx^{n-2} + ... + k$,

it will have $n$ factors of linear form, that is of the form $x - r_i$. Note that all these roots may not be real and can be imaginary number.

We will understand this part better when we learn imaginary numbers. For now we will assume and work with polynomials with only real roots.

Now, since we know that the polynomial $P(x)$ of degree $n$ can be factorised into $n$ factors, we can write:

$P(x) = (x - r_1)(x-r_2)(x - r_3)...(x - r_n)$

We can see that when $x$ takes any one of the values $r_1, r_2, ... r_n$ the term containing that particular $r_i$ becomes

$0$

Let's say $x$ takes the value $r_2$, then the term,

$x - r_2$

will become $0$.

Similarly, for any value $r_i$ of $x$, the term

$x - r_i$

will become $0$, and since one of the factors becomes $0$, the entire polynomial,

$P(x) = (x - r_1)(x-r_2)(x - r_3)...(x - r_n)$ will also become

$0$

Hence, these values $r_1, r_2\ ...\ r_n$ are are called $\underline{zeros\ of\ the\ polynomial\ P(x)}$.

Example:

Let us look at an example to understand this better:

Let us consider polynomial $P(x) = x^3 - 6x^2 - x + 30$

This is a polynomial with degree $3$ and has three factors. We can factorise this as:

$P(x) = x^3 - 6x^2 - x + 30 = (x + 2)(x - 3)(x + 5)$ and all three are real roots.

-----------book page break-----------

We can see that if we take $x$ as $-2$ or $3$ or $-5$ the value of the polynomial will become $0$.

When we draw the graph of the given polynomial it will look like the image below:

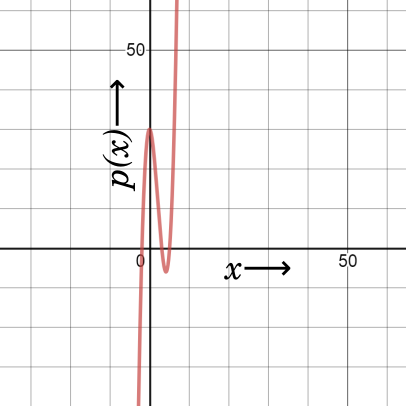
We have plotted $P(x)$ along the $Y - axis$ and $x$ along the $X - axis$

-----------book page break-----------

We can see the graph of the polynomial, (shown in red), intersects the $x$ axis at exactly $3$ points. The $y$ value, that is the value of the polynomial $P(x)$ at each of these three points equals $0$.

Intro to Polynomials -