The 3D Space
I. Introduction
So far we have been dealing with the $2D$ plane, where any specific point is uniquely identified by the $x-y$ coordinates.
In this chapter we will get introduced to the $3D$ space.
Take a look at the widget below. Try dragging the point $P$ or rotating the entire view to look at the objects from different angles.
Since a computer screen or a paper is a two-dimensional plane, what you are seeing above is the projection of the $3D$ space on your screen.
Note that although the three axes lines and the planes are shown are finite objects in the widget, in reality each on of them extends till infinity in all directions.
-----------book page break-----------
II. Euclidean Space & The Axes
Now we will take a look at how things are measured in the $3D$ space often referred to as the Euclidean Space.
Since a point is the basic formation unit for any object or shape, we will start by understanding how a point is represented in a space.
In a $2D$ plane a point is represented by two values, namely, abscissa $(x)$ and ordinate $(y)$ values. However, in a $2D$ plane no point is allowed to leave the plane. In $3D$ space there is no such restriction and a point can exist anywhere on the $xy$ plane or outside it. Therefore, we need a third measurement to tell us the deviation of the point from the $xy$ plane. This is called the $z$ value, and is measured along an axis which is perpendicular to both the $x$ and $y$ axes and passes through the origin. The $z$ axis value is sometimes called the applicate, although the terms abscissa, ordinate and applicate are rarely used in the context of measurement in the $3D$ space. They are most commonly termed as the $x$, $y$ and $z$ values.
Like the $2D$ plane, here also, the origin represents the point with all three values equal to $0$, and the origin can be chosen anywhere.
Any coordinate system, with a selected origin and set of axes, gives a valid frame of reference. But there are some conventions that are followed when choosing the directions of the axes system.
When forming an axes system, any three mutually perpendicular lines passing through a common point (origin) are taken.
You can select any two of them and mark them as two of the axes, and choose their positive directions. Once two of the axes are chosen, the positive direction of the third axes is selected using the right hand thumb rule, to satisfy the following conditions.
If you wrap your right hand fingers around the $z$ axis with your four fingers going from the positive $x$ to the positive $y$ values, then your thumb should point towards the positive $z$ axis.
-----------book page break-----------
Let us say we write this rule as:
$xy \longrightarrow z$, then all the following should also hold true.
$yz \longrightarrow x$
$zx \longrightarrow y$
Also, let us note that each of these three planes formed by selecting any two of the axes, is perpendicular to the third axis. For example, the $yz$ plane is perpendicular to the $x$ axis.
III. Dividing Planes & Octants
When working with $2D$ planes we saw that the two axes lines divide the entire plane into four infinite regions, each called a quadrant.
In case of $3D$ space the three planes form using the axes lines, divide the entire $3D$ space into $8$ infinite spaces, each called an octant.
Each of these octants have a unique combination of positive/negative coordinate values, as shown in the previous widget and the table below.
| Octant | x | y | z |
| 1st | + | + | + |
| 2nd | - | + | + |
| 3rd | - | - | + |
| 4th | + | - | + |
| 5th | + | + | - |
| 6th | - | + | - |
| 7th | - | - | - |
| 8th | + | - | - |
-----------book page break-----------
IV. Vector Representation
In $3D$ plane a point can be represented as a vector. This is done by taking the vectors $\hat{i}, \hat{j}$ and $\hat{k}$, each of length $1$ unit in the directions of positive $x$, $y$ and $z$ axes respectively.
Thus if we have a point $P = (3, 4, 5)$, using vector notation the same point can be represented as $\overrightarrow{OP} = 3\hat{i} + 4\hat{j} + 5\hat{k}$.
When we represent a point vector in a $3D$ space, the magnitude of the vector is the distance of the point from the origin. We will cover the directions of vectors and lines in details in our chapter on direction cosines.
Let us take any point $P(x, y, z)$ in the $3D$ space, and draw a cuboid, such that the origin $O$ and $P$ form the two endpoints of one of the main diagonals as shown in the figure below.
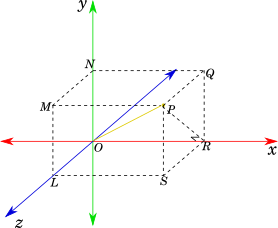
-----------book page break-----------
The diagonal $OP$ of the cuboid can be found first by finding the diagonal $PR$ of the face $PQRS$ and then applying Pythagoras theorem on $\triangle LRP$, which is right angled at $R$.
Therefore,
$PR^2 = SP^2 + SR^2 = y^2 + z^2$
and
$OP^2 = OR^2 + PR^2$
$\Rightarrow OP^2 = x^2 + y^2 + z^2$
$\therefore OP = \sqrt{x^2 + y^2 + z^2}$
This is called the magnitude of $\overrightarrow{OP}$ and is denoted by $|\overrightarrow{OP}|$
V. Distance Between Two Points
Let us try to attempt the following question.
--------- Reference to question: 96cffe0a-7336-4185-974c-f4b909a02f1f ---------
As we saw in the above problem, the distance between any two points in the $3D$ space, having coordinates $(x_1, y_1, z_1)$ and $(x_2, y_2, z_2)$ is given by $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2}$.
Observe, that the above formula is similar to the one used in two dimensions, where the distance is given by $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$.
-----------book page break-----------
VI. Other Formula Similar To 2D
There are quite a few formula that can be adapted from their counterparts in $2D$ geometry. Here are some of them.
Coordinates of a point dividing a line segment in the ratio $m:n$
For the $2D$ plane the coordinates of a point $P$ dividing the line segment formed by the joining points $(x_1, y_1)$ and $(x_2, y_2)$ is given by:
$x_p = \dfrac{x_1n + x_2m}{m + n}$ and $y_p = \dfrac{y_1n + y_2m}{m + n}$
In the $3D$ space we have,
$x_p = \dfrac{x_1n + x_2m}{m + n}$, $y_p = \dfrac{y_1n + y_2m}{m + n}$ and $z_p = \dfrac{z_1n + z_2m}{m + n}$
Similarly, a point dividing a segment externally in the ratio of $m:n$ is given by:
$x_p = \dfrac{mx_2 - nx_1}{m - n}$, $y_p = \dfrac{my_2 - ny_1}{m - n}$ and $z_p = \dfrac{mz_2 - nz_1}{m - n}$
Centroid of a two-dimensional triangle formed by $(x_1, y_1)$, $(x_2, y_2)$ and $(x_3, y_3)$ is given by,
$x_c = \dfrac{x_1 + x_2 + x_3}{3}$ and $y_c = \dfrac{y_1 + y_2 + y_3}{3}$
Similarly, the centroid of a triangle in the three dimensional space is given by:
$x_c = \dfrac{x_1 + x_2 + x_3}{3}$, $y_c = \dfrac{y_1 + y_2 + y_3}{3}$ and $z_c = \dfrac{z_1 + z_2 + z_3}{3}$