Distance Of A Line From A Point
Given point $P$ with coordinates $x_1, y_1$ and line $AB$ represented by $ax + by + c = 0$ such that $P$ lies outside $AB$, that is,
$ax_1 + by_1 + c \ne 0$
Let $PC$ be a perpendicular drawn from $P$ on $AB$ as shown in the following figure:
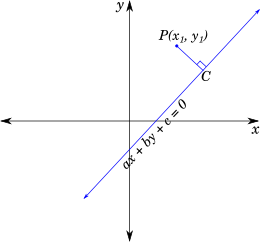
We need to find the length of $PC$.
Slope of the line $AB$ is $-\dfrac{a}{b}$
Therefore, the slope of the line $PC$ is $\dfrac{b}{a}$
-----------book page break-----------
The equation of the line $PC$ is:
$y - y_1 = \dfrac{b}{a}(x-x_1)$
$\Rightarrow ay - ay_1 = bx - bx_1$
$\Rightarrow bx - ay + ay_1 - bx_1 = 0$ $...\ eqn(i)$
The line $AB$ is represented by:
$ax + by + c = 0$ $...\ eqn(ii)$
We can find the coordinates of the intersection point $C$ by solving the two equations $(i)$ and $(ii)$ as follows:
Adding $b \times (i) + a \times (ii)$ we get:
$b^2x - \cancel{aby} + aby_1 - b^2x_1 + a^2x + \cancel{aby} + ac = 0$
$\Rightarrow x(a^2 + b^2) = b^2x_1 - aby_1 - ac$
$\Rightarrow x = \dfrac{b^2x_1 - aby_1 - ac}{a^2 + b^2}$
Similarly, using $b \times (ii) - a \times (i)$ we get:
$\cancel{abx} + b^2y + bc - \cancel{abx} + a^2y - a^2y_1 + abx_1 = 0$
$\Rightarrow y(a^2 + b^2) = a^2y_1 - abx_1 -bc$
$\Rightarrow y = \dfrac{a^2y_1 - abx_1}{a^2 + b^2}$
Therefore, the length $l$, of the line segment $PC$ is given by:
$l = \sqrt{\left(\dfrac{b^2x_1 - aby_1 - ac}{a^2 + b^2} - x_1\right)^2 + \left(\dfrac{a^2y_1 - abx_1 -bc}{a^2 + b^2} - y_1\right)^2}$
-----------book page break-----------
$= \sqrt{\left(\dfrac{\cancel{b^2x_1} - aby_1 - ac - a^2x_1 - \cancel{b^2x_1}}{a^2 + b^2} \right)^2 + } $ $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \overline{\left(\dfrac{\cancel{a^2y_1} - abx_1 - \cancel{a^2y_1} - b^2y_1}{a^2 + b^2}\right)^2}$
$= \sqrt{\dfrac{( - aby_1 - ac - a^2x_1)^2 + (- abx_1 - b^2y_1 - bc)^2}{(a^2 + b^2)^2}}$
$= \sqrt{\dfrac{(aby_1 + ac + a^2x_1)^2 + (abx_1 + b^2y_1 + bc)^2}{(a^2 + b^2)^2}}$
$= \sqrt{\dfrac{a^2b^2y_1^2 + a^2c^2 + a^4x_1^2 + 2a^2bcy_1 + 2a^3cx_1 + }{(a^2 + b^2)^2}} $ $\ \ \ \ \ \ \ \ \ \ \ \ \dfrac{\overline{2a^3bx_1y_1 + a^2b^2x_1^2 + b^4y_1^2 + b^2c^2 + 2ab^3x_1y_1 + 2ab^2cx_1 + 2b^3cy_1}}{\ }$
$= \sqrt{\dfrac{(a^4x_1^2 + a^2b^2y_1^2 + a^2c^2 + 2a^3bx_1y_1 + 2a^3cx_1 + 2a^2bcy_1)\ + }{(a^2 + b^2)^2}} $ $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \dfrac{\overline{(a^2b^2x_1^2 + b^4y_1^2 + b^2c^2 + 2ab^3x_1y_1 + 2ab^2cx_1 + 2b^3cy_1)}}{\ }$
-----------book page break-----------
$= \sqrt{\dfrac{a^2(a^2x_1^2 + b^2y_1^2 + c^2 + 2abx_1y_1 + 2acx_1 + 2bcy_1)\ +}{(a^2 + b^2)^2}} $ $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \dfrac{\overline{b^2(a^2x_1^2 + b^2y_1^2 + c^2 + 2abx_1y_1 + 2acx_1 + 2bcy_1)}}{\ }$
$= \sqrt{\dfrac{\cancel{(a^2 + b^2)}(a^2x_1^2 + b^2y_1^2 + c^2 + 2abx_1y_1 + 2acx_1 + 2bcy_1)}{(a^2 + b^2)^\cancel{2}}}$
$= \sqrt{\dfrac{(ax_1 + by_1 + c)^2}{(a^2 + b^2)}}$
$= \dfrac{ax_1 + by_1 + c}{\sqrt{a^2 + b^2}}$
Since $ax_1 + by_1 + c$ can be either positive or negative based on which side of the line the point $x_1, y_1$ lies, we should take the absolute value of the numerator to get a positive value for the distance.
Therefore,
$l = \dfrac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}$