Basic Trigonometric Identities

We learnt about trigonometric ratios .

Today we will learn about some basic identities involving trigonometric ratios.

Let us take a look at the figure of the right angled triangle $ABC$ below, with $\angle B = 90^\circ$ and we will use the trigonometric ratios for $\angle A$:

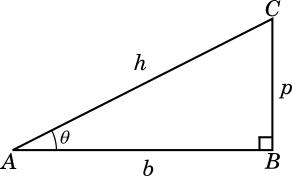
$\underline{I.\ Definitions}$

We will do a quick listing of the definitions of various trigonometric ratios below:

$sin(A) = \dfrac{p}{h}$, $cos(A) = \dfrac{b}{h}$, $tan(A) = \dfrac{p}{b}$

$cosec(A) = \dfrac{h}{p}$, $sec(A) = \dfrac{h}{b}$, $cot(A) = \dfrac{b}{p}$

-----------book page break-----------

$\underline{II.\ Derivations}$

Applying Pythagoras theorem to our right angled triangle we get:

$p^2 + b^2 = h^2$

Dividing both sides by $h^2$ we get:

$\dfrac{p^2}{h^2} + \dfrac{b^2}{h^2} = \dfrac{h^2}{h^2}$

$\Rightarrow \left(\dfrac{p}{h}\right)^2 + \left(\dfrac{b}{h}\right)^2 = 1$

Replacing $\dfrac{p}{h} = sin(A)$ and $\dfrac{b}{h} = cos(A)$, we get:

$\left\{sin(A)\right\}^2 + \left\{cos(A)\right\}^2 = 1$

$\left\{sin(A)\right\}^2$ is also written as $sin^2(A)$, which is the commonly accepted way of writing powers of trigonometric ratios.

$\therefore sin^2(A) + cos^2(A) = 1$

-----------book page break-----------

Now, dividing the same Pythagoras relationship by $b^2$ we get:

$\dfrac{p^2}{b^2} + \dfrac{b^2}{b^2} = \dfrac{h^2}{b^2}$

$\Rightarrow \left(\dfrac{p}{b}\right)^2 + 1 = \left(\dfrac{h}{b}\right)^2$

Now replacing $\dfrac{p}{b} = tan(A)$ and $\dfrac{h}{b} = sec(A)$ we get:

$tan^2(A) + 1 = sec^2(A)$

$\Rightarrow tan^2(A) = sec^2(A) - 1$

Now, again dividing the Pythagoras relationship by $p^2$, we get:

$\dfrac{p^2}{p^2} + \dfrac{b^2}{p^2} = \dfrac{h^2}{p^2}$

$\Rightarrow 1 + \left(\dfrac{b}{p}\right)^2 = \left(\dfrac{h}{p}\right)^2$

Replacing, $\dfrac{b}{p} = cot(A)$ and $\dfrac{h}{p} = cosec(A)$, we get:

$1 + cot^2(A) = cosec^2(A)$

$cot^2(A) = cosec^2(A) - 1$

-----------book page break-----------

$\underline{III.\ Summary}$

Let us quick summarise the trigonometric identities we derived in the previous section:

$sin^2(A) + cos^2(A) = 1$

$tan^2(A) = sec^2(A) - 1$

$cot^2(A) = cosec^2(A) - 1$