Altitudes & Orthocentre Of Triangles
In this topic we will learn about the altitudes of a triangle and its orthocentre.
The altitudes of any triangle are concurrent, that is, they pass through a common point. We will see the proof of this below.
We can take any triangle $ABC$, and draw the altitude $BQ$ from vertex $B$ to $CA$ and the altitude $CR$ from vertex $C$ to $AB$. Let's say they intersect at point $O$. We join $AO$ and extend the line to meet $BC$ at point $P$.
If we are able to show that $AP$ is perpendicular to $BC$ then we would have proven that $AP$ is an altitude and that the three altitudes are concurrent.
-----------book page break-----------
$\underline{Construction:}$
Through each of the vertices $A$, $B$ and $C$ draw lines parallel to the opposite side of that vertex. Let's call the intersections of these lines as $X$, $Y$ and $Z$. Let us join points $X$, $Y$ and $Z$ with point $O$. We will get a figure similar to the one shown below:
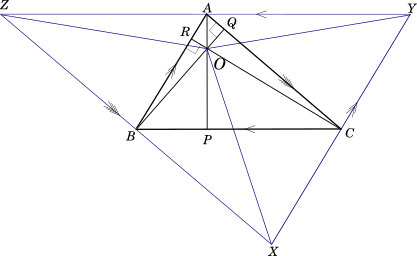
$\underline{Proof:}$
Consider $\triangle$s $ABC$ and $XCB$
$XY \parallel AB$ and $BC \parallel YZ$ by construction.
$\texttip{\therefore}{therefore}$ $ABCY$ is a parallelogram.
$\texttip{\because}{because}$ Opposite sides of a parallelogram are equal,
$BC = AY$.
-----------book page break-----------
Similarly $BCAZ$ is also a parallelogram,
$\texttip{\therefore}{therefore} BC = AZ$.
Thus we get $BC = AY = AZ$, $\texttip{\therefore}{therefore} A$ is the midpoint of $YZ$
Similarly, we can show that $B$ is the midpoint of $ZX$ and $C$ is the midpoint of $XY$
$\texttip{\because}{because} BQ \perp AC$ and $AC \parallel ZX$, $BQ$ is also perpendicular to $ZX$.
$\texttip{\therefore}{therefore} BQ$ is the perpendicular bisector of $ZX$
Similarly, $CR$ is the perpendicular bisector of $XY$.
Therefore, $O$ is the circumcentre of $\triangle XYZ$
Therefore $AO$ is the perpendicular bisector of $YZ$, since $A$ is the midpoint of $YZ$ and we have proven , that the perpendicular bisectors of a triangle are concurrent.
Since $AO \perp YZ$ and $BP \parallel YZ$, $OP$ is also perpendicular to $BC$.
Therefore $AP$ is the altitude of $\triangle ABC$ from vertex $A$ to $BC$.
-----------book page break-----------
$\underline{Properties\ of\ Orthocenter:}$
$\bullet$ For an acute angle triangle the orthocentre lies inside the triangle.
$\bullet$ For a right angled triangle the orthocenter is the $90^\circ$ vertex.
$\bullet$ For an obtuse angled triangle the orthocentre lies outside the circle.
$\bullet$ The angle subtended by any side with the orthocentre and with the opposite vertex are supplementary. In our diagram above:
$\angle BOC + \angle BAC = \angle AOC + \angle ABC = \angle AOB + \angle ACB = 180^\circ$
$\bullet$ The orthocentre divides the altitudes in line segments, who product is constant for all the altitudes. In our diagram:
$AO \times OP = BO \times OQ = CO \times OR$
$\bullet$ The reflection of the orthocentre about any of the sides of the triangle lies on the circumcircle.