Conditional Probability
I. Introduction
A common source of confusion in statistical probability is the difference between Independent Events and Mutually Exclusive events.
These two concepts imply quite different things, and in the next two sections we will clarify these.
II. Dependent & Independent Events
Let us understand this better using an example. Let us consider the following two scenarios:
$\underline{\text{Case A:}}$
- You are drawing cards from a normal deck of $52$ cards, each time returning the drawn card to the deck before drawing the next card.
$\underline{\text{Case B:}}$
- You are drawing cards from a normal deck of $52$ cards, each time discarding the drawn card, and then drawing the next card.
The question is what is the probability of drawing two successive red cards in the first two draws?
It is easy to see that the probability of the desired outcome of the first draw are identical in both cases, because in each of these cases the condition of the deck of cards are identical.
However, the second draw will have different probabilities in each of the above cases.
-----------book page break-----------
In $\underline{\text{Case A:}}$ the drawn card is being returned to the deck. Therefore, the condition of the deck is same as the first draw, which results in an unchanged probability of various outcomes in the second draw.
The probability of getting a red card is
$\dfrac{26}{52}$
in any of the outcomes.Whereas, in $\underline{\text{Case B:}}$, if the probability of getting a red card in the first draw is $\dfrac{26}{52}$ and the probability of getting a red card in the second draw, given that the first draw was a red card, is
$\dfrac{25}{51}$
.Therefore, the probability of getting two successive red cards are
$\dfrac{26}{52} \times \dfrac{25}{51}$
Now, it is easy to see that in $\underline{\text{Case B:}}$ the probabilities of various outcomes of each draw changes depending on the result of the previous draw. Drawing a black card increases the probability of a red card in the next round, while drawing a red card reduces the probability of drawing a red card in the next round.
So, the outcomes of each draw for $\underline{\text{Case A:}}$ are independent events, whereas the outcomes of each draw in $\underline{\text{Case B:}}$ are dependent events.
Put using notations of probability, we can say that, if events $A$ and $B$ are independent, then:
$P(A) = P(A | B)$, that is, the probability of event $A$ is same as probability of $A$ given the fact the event $B$ has occurred, in other words, the occurrence of $B$ has no bearing on the occurrence of $A$.
-----------book page break-----------
III. Mutually Exclusive & Overlapping Events
Mutually exclusive events are the ones that have a null intersection.
For example, in a roll of a die, the event that the outcome is an odd number vs the event that the outcome is an even number, are mutually exclusive.
That is, there is no way these two could occur together. Whereas, the events that the outcome is a prime number and the outcome is an even number are not mutually exclusive. Because there is a case where both can happen together, that is, if the outcome is a $2$, then both events would have occurred together.
If $A$ is the set of all events of type $a$ and $B$ be the set of events $b$, then if $A$ and $B$ are mutually exclusive, then $A \cap B =$
$\phi$
and $A \cap B \ne$ $\phi$
for non-exclusive events $A$ and $B$.-----------book page break-----------
IV. Conditional Probability
We will understand this concept using a problem.
Consider the following case:
A clinic tests a patient for vitamin K deficiency using a blood test. $10\%$ of a given population has vitamin K deficiency. The blood test gives the following accuracy levels:
If a patient has vitamin K deficiency then the test gives a positive result with $98\%$ probability.
If a patient doesn't have vitamin K deficiency, then the test gives a negative result with a $95\%$ probability.
(Assume that there is no other symptom of vitamin K deficiency)
A person, selected at random, is tested positive for vitamin K deficiency. What is the probability that has actually has vitamin K deficiency?
To solve this problem, we will take a step by step approach, and split up each step into a question, that needs to be answered
-----------book page break-----------
--------- Reference to question: 10415ac1-3c38-4b82-a5ca-aa2178e862ed ---------
Now, let us let us extend the tree as shown below, and denote the event that somebody tests positive for vitamin K deficiency as $(+)$. Therefore, based on the given fact, $P(+ | K) = 0.98$. The $\unicode{0x201C}|\unicode{0x201D}$ symbol denotes "given some fact".
In this case $P(+ | K)$ denotes the probability of test showing positive result, given the person has K deficiency, is $0.98$ and $P(- | K)$ denotes the probability of test showing negative result, given the person is actually vitamin K deficient.
--------- Reference to question: a9d37e5b-f9bc-4e6b-bbbc-8a31e6805dd4 ---------
Moving on to the final expansion of the tree, it is given that $P(- | \lnot K) = 0.95$
-----------book page break-----------
--------- Reference to question: 085447c1-4631-4614-9cc2-b65a35ddd17d ---------
-----------book page break-----------
Now that we have completed our tree which looks like:
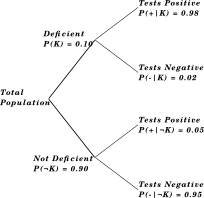
let us try to answer our original question.
--------- Reference to question: cf0bdc48-321e-40ec-891f-e84a54fb5eba ---------
Like we used a tree to solve this problem, we can also use a tabular structure to solve the same problem. Let us take a sample population of $1000$
We can break up the number as follows:
$90\%$ of $1000$ do not have $K$ deficiency, therefore $900$ do not have $K$ deficiency whereas $100$ have $K$ deficiency.
Out of the $900$ that do not have $K$ deficiency, $95\%$, that is $855$ test positive and $5\%$, that is, $45$ will test positive (false positive).
Out of the $100$ that have $K$ deficiency, $98\%$, that is $98$ will test positive while the remaining $2$ will test negative (false negative).
Thus our table will look like:
| $K$ | $\lnot K$ | Total | |
| $+$ | $98$ | $45$ | $143$ |
| $-$ | $2$ | $855$ | $857$ |
| Total | $100$ | $900$ | $1000$ |
-----------book page break-----------
Of the total $143$ people that tested positive, $98$ actually has vitamin $K$ deficiency.
Therefore the required probability is:
$\dfrac{98}{143} = 0.6853 \approx 0.69$
Discrete Probability