Introduction To Set Operations
As with normal numbers, we can perform various operations on sets. The operations we are going to look at today are Intersection, Union and Complement. These are all binary operators, that is, they need two operands to operate.
Union:
We use the symbol $\unicode{0x201C} \cup \unicode{0x201D}$ to denote the union operation.
We can combine two sets defined by two different properties, to get a third meaningful set.
For example:
We can define set $A$ as the set of all prime number less than 10.
We can define set $B$ as the set of all odd numbers less than 10.
Therefore,
$A = \{2, 3, 5, 7\}$
$B = \{1, 3, 5, 7, 9\}$
When we create the union of these two sets they will contain all elements in either set A or set B or both of them. Elements occurring in both the set will appear only once and NOT twice. So,
$C = A \cup B = \{1, 2, 3, 5, 7, 9\}$
A good way of looking at union is to say, elements that belong to set $A$, or to set $B$, or both is a member of the resulting set $C$.
In our example we can say the resulting set C is a set of numbers less than 10 that are either prime or odd.
-----------book page break-----------
Intersection:
We use the symbol $\unicode{0x201C} \cap \unicode{0x201D}$ to denote the intersection operation.
Intersection between two sets results into a set containing elements that are present in BOTH sets. If it is absent in any one of the sets, it is not an element of the intersection.
If we take the same definition of set $A$ and set $B$ from the union example,
$A = \{2, 3, 5, 7\}$
$B = \{1, 3, 5, 7, 9\}$
$C = A \cap B = \{3, 5, 7\}$
A good way of looking at intersection is to say, elements that belong to set $A$ AS WELL AS to set $B$ is a member of the resulting set $C$.
In our example we can say the resulting set, $C$ is a set of numbers less than 10 that are prime as well as odd.
Complement (also known as Subtraction):
We use the symbol $\unicode{0x201C}\ \unicode{0x5C} \unicode{0x201D}$ to denote the complement operation, but we can also use the normal subtraction symbol $-$ to denote complement or subtraction.
This result for the operation $A - B$ (or $A\unicode{0x5C}B$) is obtained by removing from set $A$, all the elements that appear in both $A$ and $B$.
We go back to our original example, where:
$A = \{2, 3, 5, 7\}$
$B = \{1, 3, 5, 7, 9\}$
To calculate $A - B$, we need to remove elements $3$, $5$ and $7$ from $A$, since they appear in both $A$ and $B$.
So what we get is:
$C = A - B = \{2\}$
-----------book page break-----------
Like in ordinary number subtraction $A - B$ is not equal to $B - A$, unless both sets are equal.
In this case if we were to calculate $B - A$, instead or $A - B$, result $C$ would be:
$C = B - A = \{1, 9\}$
Here we removed from set $B$, the elements that appear in both $A$ and $B$.
We can describe this using properties defining our sets, by say the resultant set $C$ is a set of all numbers less than $10$ that are prime and NOT odd.
Some Important Relationships:
For this we will use our previous definitions of set $A$ and $B$, such that:
$Set\ A = $ all prime numbers less than $10$ = $\left\{2,\ 3,\ 5,\ 7\right\}$, and
$Set\ B = $ all odd numbers less than $10$ = $\left\{1,\ 3,\ 5,\ 7,\ 9\right\}$
If we draw the Venn Diagram of the above sets, we get the following figure:
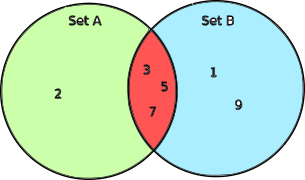
-----------book page break-----------
Recollect from , that the cardinality of a set is the count of the elements in the set and is denoted by two $\unicode{0x201C}\ |\ \unicode{0x201D}$ symbols.
Hence, from our definitions $|A| = 4$, $|B| = 5$ and $|A \cap B| = 3$
$\underline{Relationship:\ 1}$
$|A \cup B| = |A| + |B| - |A \cap B|$
As we can see, from the Venn Diagram if we add $|A|$ and $|B|$ the elements of the set $A \cap B$ gets counted twice.
Therefore, we need to subtract $|A \cap B|$ once from $|A| + |B|$ to get $|A \cup B|$
In our example,
$|A \cup B| = |A| + |B| - |A \cap B| = 4 + 5 - 3 = 6$
We can actually count and see that the count of elements in the three regions combined in the diagram, is $6$
$\underline{Relationship:\ 2}$
$|A - B| = |A| - |(A \cap B)|$
By definition, $A - B$ is the set that we get by removing all the elements that are common in both $A$ and $B$ from set $A$.
Therefore, in our example:
$|A - B| = |A| - |(A \cap B)| = 4 - 3 = 1$
In the Venn Diagram above, $A - B$ is denoted by the region in green.
Can you verify this formula by calculating $|B - A|$?