Angles Of A Polygon
I. Introduction
Here we will learn about the angles of a polygon. Suppose we take an $N$ sided polygon. How many angles does it have?
It has
$N$
internal angles. For example a triangle is a $3$ sided polygon and has $3$ internal angles, a quadrilateral has $4$ sides and $4$ internal angles, likewise an $N$ sided polygon will have $N$ angles.Today we will learn about some properties of these angles.
We already know that the sum of all the angles of a triangle is
$180^{\circ}$
and the sum of all the angles of a quadrilateral is $360^{\circ}$
.What about a general $N$ sided polygon?
II. Sum Of Internal Angles Of A Polygon
In the figures below, we have shown a pentagon and a general $N$ sided polygon.
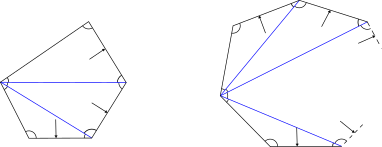
First we choose random vertex, and then from it draw diagonals to all the remaining vertices. How many triangles are formed? In case of the pentagon there will be $3$ triangles, and for the $N$ sided polygon it is easy to see that there will be $N - 2$ such triangles.
-----------book page break-----------
That is because any vertex will have two adjacent sides, and the remaining $N-2$ non-adjacent sides will form a triangle with this vertex. In the given figures the non-adjacent sides are shown with the ${-}{\unicode{x25B6}}$ sign.
The sum of the angles of the pentagon and the $N$ sided polygon is equal to the sum of the angles of all the triangles thus formed.
We have seen , that the sum of all the angles of a triangle is
$180^{\circ}$
.Therefore, the sum of all the angles of the pentagon is $3 \times 180 = 540^{\circ}$ since there are $3$ triangles, and the sum of the angles of the $N$ sided polygon is
$(N-2) \times 180^{\circ}$
, since it has $N-2$ triangles in all.III. Internal Angles Of A Regular Polygon
Now, if the given $N$-sided polygon is a regular polygon, all the angles will be of equal magnitude, hence each angle will be
$\dfrac{(N-2) 180}{N}$
$= \dfrac{180 \times N - 2 \times 180}{N}$
$= 180 - \dfrac{360}{N}$
-----------book page break-----------
IV. Sum Of External Angles Of A Polygon
The external angle of a polygon is defined as the angle formed by extending any one side of the polygon and the side adjacent to this side as shown in the figure below with a $\circ$ sign.
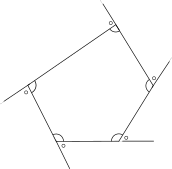
The sum of any of the internal angles and its corresponding external angle is always
$180^{\circ}$
.For an $N$ sided polygon, there are $N$ such external and internal angle pairs.
Sum of all these pairs =
$N \times 180^{\circ}$
As we have seen before, the sum of all the internal angles = $(N-2) \times 180^{\circ}$
Therefore, sum of all the external angles of a polygon is equal to:
$N \times 180^{\circ} - (N - 2) \times 180^{\circ}$
$= N \times 180^{\circ} - N \times 180^{\circ} + 2 \times 180^{\circ}$
$= 2 \times 180^{\circ}$
$= 360^{\circ}$
-----------book page break-----------
In other words we can say:
$\unicode{x201C}\text{For any N-sided polygon,}$ $\text{the sum of the external angles is }360^\circ \text{, irrespective of the value of N}\unicode{x201D}$
Polygons & Lines Of Symmetry -
Polygons Definitions -