Area Of Triangles And The Sine Rule

$\underline{Theorem}$

The area of a triangle $ABC$, can be found given any two sides and the included angle can be found using the formula:

$ar[\triangle ABC] = \dfrac{1}{2} AB.AC.sinA$

The $Sine\ Rule$ states that:

$\dfrac{sinA}{a} = \dfrac{sinB}{b} = \dfrac{sinC}{c}$, where $A$, $B$ and $C$ are the three angles of a triangle, and $a$, $b$ and $c$ are the sides opposite to vertices $A$, $B$ and $C$ respectively.

$\underline{Construction}$

Let us draw $\triangle ABC$ with $BE$ as the altitude from vertex $B$ to $AC$, as shown below:

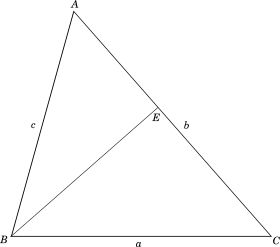
-----------book page break-----------

$\underline{Proof}$

We know that the $ar[ABC] = \dfrac{1}{2} AC \times BE$ $...eqn\ (i)$

We know that $\dfrac{BE}{AB} = sinA \Rightarrow BE = ABsinA$

Replacing $BE$ in $eqn\ (i)$ we get:

$ar[\triangle ABC] = \dfrac{1}{2} AC.ABsinA$

We can now derive the $Sine\ Rule$ using the area formula directly.

$ar[\triangle ABC] = \dfrac{1}{2} AB.AC.sinA = \dfrac{1}{2} BC.BA.sinB = \dfrac{1}{2} CB.CA.sinC$

$\Rightarrow c.b.sinA = a.c.sinB = a.b.sinC = 2\times ar[\triangle ABC]$

Dividing everything by $abc$, we get:

$\dfrac{sinA}{a} = \dfrac{sinB}{b} = \dfrac{sinC}{c} = \dfrac{2\times ar[\triangle ABC]}{abc} = constant$