Understanding Angles As Ratios

So far we have studied angles as the movement of one arm about another arm. Today we are going to look at angles from another perspective.

I. Understanding Radians

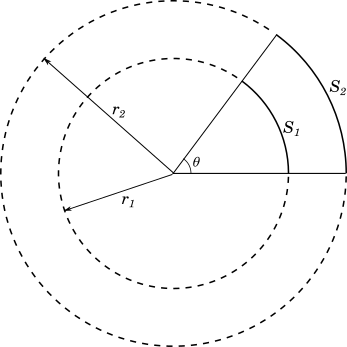
An angle can be defined as the ratio of an arc to that of the radius. The diagram below shows two concentric circles.

-----------book page break-----------

The smaller circle has a radius of $r_1$ and the larger circle has a radius of $r_2$.

The length of an arc, $S$, is proportional to the length of the radius $r$ and the angle of the arc $\theta$, that is:

$S \propto r$ and $S \propto \theta$,

$\Rightarrow S \propto r\theta$

$\Rightarrow S = kr\theta$

Now, if we choose the unit of angle such that $1$ unit angle is the angle subtended at centre by an arc of length equal to the radius, that is $S = r$, we get:

$r = kr\times 1$

$\Rightarrow k = 1$

That is exactly how we get the definition of a $radian$:

One radian is the angle subtended at the centre by an arc of length equal to the radius of the circle.

The relationship $S = r\theta$ is valid when $\theta$ is expressed in $radians$

Like degree is denoted by $^\circ$ next to the value of the angle, radian is denoted by $^c$ next to the value of the angle.

For example, $\angle ABC = 1.2^c$.

In general, if the degree sign is missing after the magnitude of an angle, it is taken as a radian value.

So, when we say $\angle PQR = \dfrac{\pi}{4}$ it would mean that the angle is $\dfrac{\pi}{4}$ radians, and not degree.

The ratio of the length of the circumference of a circle to that of the diameter of the circle is taken as $\pi$, which is an irrational number, whose value is a approximated as $\dfrac{22}{7}$ or $3.1416$. Of course, there are many other approximations available in both decimal or fraction format.

-----------book page break-----------

That's where we get the formula for the circumference of a circle.

$\pi = \dfrac{C}{d}$ where $C$ is the circumference of the circle.

$\Rightarrow C = \pi \times d$

$\Rightarrow C = \pi \times 2r$

$\Rightarrow C = 2\pi r$

While converting radians to degree or vice versa, you may want to remember the $\pi = 180^\circ = a\ straight\ angle$

II. Negative Angles

Till now we have seen that angles have a magnitude, but angles have a direction as well, and hence there can be positive and negative angles.

Take a look at the following diagram:

-----------book page break-----------

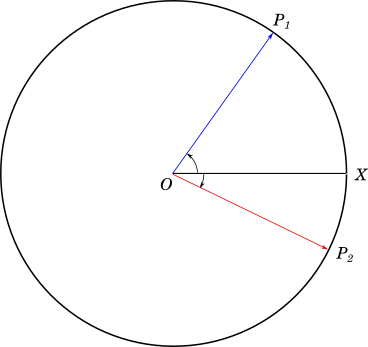
The angle $XOP_1$ is formed by rotating line $OP$ about the centre $O$ in the anti-clockwise direction from the fixed line $OX$. This direction is taken as a positive direction for angles.

While $\angle XOP_2$ is formed by rotating line $OP$ about the same centre, but in the clockwise direction. This is taken as the negative direction for angles, hence $\angle XOP_2$ has a negative value, and $\angle XOP_1$ has a positive value.

The horizontal direction toward the right (positive $X$ axis direction), is taken as $0$.

-----------book page break-----------

III. Angles > 360^o

In the diagram below the line $OP$ is rotating about the centre $O$ in the positive direction starting at an angle of $0^\circ$. At each step it rotates by $70^\circ$. $OX$ is a fixed line.

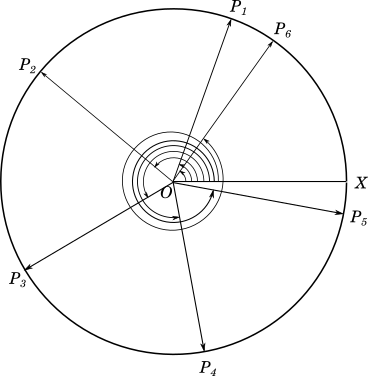
Hence $\angle XOP_1 = 70^\circ$, $\angle XOP_2 = 140^\circ$, $\angle XOP_3 = 210^\circ$, $\angle XOP_4 = 280^\circ$ and $\angle XOP_5 = 350^\circ$.

-----------book page break-----------

What happens when the arm $OP$ moves by another $70^\circ$? How much is $\angle XOP_6$?

It goes to $350 + 70 = 420^\circ$, and yes, we can have angles greater than $360^\circ$.

The final angle magnitude in degrees, measured from the $0^\circ$ position can be done by taking the remainder of the angle magnitude divided by $360$.

For example the angle $420^\circ$ is equivalent to $420\ mod\ 360 = 60^\circ$ ($mod$ denotes the remainder operation)