Apollonius's Theorem

$\underline{Theorem}$

Apollonius's Theorem states that for any $\triangle ABC$, if $AD$ is the median from $A$ to $BC$ then the following relationship holds:

$AB^2 + AC^2 = 2\left\{AD^2 + \left(\dfrac{BC}{2}\right)^2\right\}$.

$\underline{Construction}$

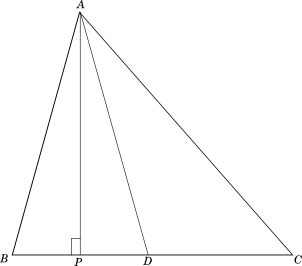
Let $ABC$ be the given triangle with $AD$ as the median from $A$ to $BC$. Let $AP$ be the altitude drawn from $A$ to $BC$, as shown in the diagram below.

-----------book page break-----------

$\underline{Proof}$

$\because D$ is the midpoint of $BC$,

$BD = CD = \dfrac{BC}{2}$

$BP + CP = BC$

Since, $\angle APB = 90^\circ$,

$AB^2 = AP^2 + BP^2$

$AC^2 = AP^2 + CP^2$

$AD^2 = AP^2 + PD^2$

$\therefore AB^2 + AC^2 = 2AP^2 + BP^2 + CP^2$

$\Rightarrow AB^2 + AC^2 = 2(AD^2 - PD^2) + BP^2 + CP^2$

$\Rightarrow AB^2 + AC^2 = 2AD^2 - 2PD^2 + BP^2 + CP^2$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + BP^2 - PD^2 + CP^2 - PD^2$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + (BP - PD)(BP + PD)$$\ \ \ + (CP - PD)(CP + PD)$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + (BP - PD)BD + CD(CP + PD)$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + (BP - PD)BD + BD(CP + PD)$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + BD(BP - PD + CP + PD)$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + BD(BP + CP)$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + BD.BC$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + \dfrac{BC}{2}BC$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + \dfrac{BC^2}{2}$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + 2\dfrac{BC^2}{4}$

$\Rightarrow AB^2 + AC^2 = 2AD^2 + 2\left(\dfrac{BC}{2}\right)^2$

-----------book page break-----------

$\therefore AB^2 + AC^2 = 2\left\{AD^2 + \left(\dfrac{BC}{2}\right)^2\right\}$

$\underline{Corollary\ 1\ \ Relationship\ Between\ 3\ Sides\ And\ The\ Medians:}$

We can find a useful relation between the three sides of the triangle as a result of this theory.

If we take the $AD$, $BE$ and $CF$ as the $3$ medians of $\triangle ABC$,

then using Apollonius's Theorem for each of the medians we get:

$AB^2 + AC^2 = 2\left\{AD^2 + \left(\dfrac{BC}{2}\right)^2\right\}$

$BC^2 + CA^2 = 2\left\{CF^2 + \left(\dfrac{AB}{2}\right)^2\right\}$

$AB^2 + BC^2 = 2\left\{BE^2 + \left(\dfrac{CA}{2}\right)^2\right\}$

Adding the three equations above, we get:

$2AB^2 + 2BC^2 + 2CA^2 = 2AD^2 + 2BE^2 + 2CF^2 + 2\dfrac{AB^2 + BC^2 + CA^2}{4}$

$\Rightarrow 2(AB^2 + BC^2 + CA^2) - \dfrac{AB^2 + BC^2 + CA^2}{2} = 2(AD^2 + BE^2 + CF^2)$

$\Rightarrow \dfrac{3(AB^2 + BC^2 + CA^2)}{2} = 2(AD^2 + BE^2 + CF^2)$

$\Rightarrow 3(AB^2 + BC^2 + CA^2) = 4(AD^2 + BE^2 + CF^2)$