Angle Bisectors & Incentre Of Triangles

We will understand some of the properties of angle bisectors of a triangle.

Out of these, the main theorem states that:

$\unicode{0x201C}\underline{Bisectors\ Of\ The\ 3\ Angles\ Of\ Triangle\ Meet\ At\ A\ Common\ Point\ }\unicode{0x201D}$.

We will begin by proving this theorem.

I. Construction

Let us construct any triangle $ABC$, and draw the bisectors of $B$ and $C$, and call their intersection point as $I$.

We join points $A$ and $I$ to get $AI$. If we are able to prove that $AI$ is the bisector of $\angle A$ then we would have proven that all three angle bisectors of a triangle passes through a common point.

Let us do the following constructions:

From point $I$ draw perpendiculars to sides $AB$, $BC$ and $CA$ at $P$, $Q$ and $R$ respectively, as shown in the following figure.

-----------book page break-----------

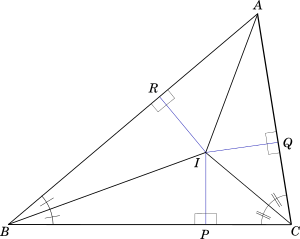
Proof:

Consider $\triangle IPC$ and $\triangle IQC$.

$\angle IPC = \angle IQC$ $\texttip{\because}{because}$ $IP$ and $IQ$ are perpendiculars to $BC$ and $CA$.

$IC$ is common to both triangles.

$\angle PCI = \angle QCI$ $\texttip{\because}{because}$ $CI$ bisects $\angle PCQ$

$\texttip{\therefore}{therefore} \triangle PCI \texttip{\cong}{congruent to} \triangle QCI$, using the $AAS$ rule

$\texttip{\Rightarrow}{follows that} IP = IQ$

Using similar steps we can prove that $\triangle PBI \texttip{\cong}{congruent to} \triangle RBI \texttip{\Rightarrow}{follows that} IR = IP$

$\texttip{\therefore}{therefore} IP = IQ = IR$

Now, consider $\triangle ARI$ and $\triangle AQI$

$IR = IQ$

Hypotenuse $AI$ is common to both triangles.

-----------book page break-----------

Using the $RHS$ rule, $\triangle ARI \texttip{\cong}{congruent to} \triangle AQI$

$\texttip{\Rightarrow}{follows that} \angle IAR = \angle IAQ$

$\texttip{\therefore}{therefore} IA$ bisects $\angle A$

Now let us look at some important properties of the angle bisectors.

Corollary-1

If you draw a circle with the point $I$ as the centre and any one of $IP$, $IQ$ or $IR$ as the radius, it will pass through all the three points $P$, $Q$ and $R$ since $IP = IQ = IR$.

This circle is called the $\unicode{0x201C}incircle\unicode{0x201D}$ of $\triangle ABC$ and point $I$ is called the $\unicode{0x201C}incentre\unicode{0x201D}$ of $\triangle ABC$. The radius of the incircle is called the $\unicode{0x201C}inradius\unicode{0x201D}$

The incircle is shown in dotted line in the following diagram:

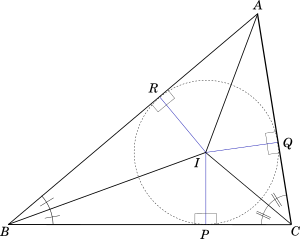
-----------book page break-----------

Corollary-2

The angle bisector of any angle of a triangle divides the opposite side in the ratio of the remaining two sides.

For example, in our figure if we extend $AI$ to meet $BC$ at $T$, as shown in the figure below, then

$\dfrac{BT}{CT} = \dfrac{AB}{AC}$

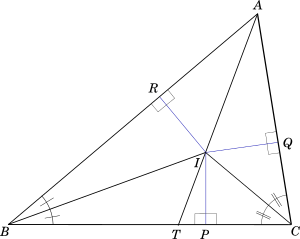
-----------book page break-----------

Corollary-3

As we know, every triangle has $3$ altitudes, one from each vertex to its opposite side.

If we take the altitudes as $h_1$, $h_2$ and $h_3$ and the inradius as $r$, then:

$\dfrac{1}{h_1} + \dfrac{1}{h_2} + \dfrac{1}{h_3} = \dfrac{1}{r}$

Corollary-4

If $s$ is the semiperimeter of a triangle and $r$ is the inradius, then,

the area of the triangle = $sr$.

You may note that a polygon with number of sides $n \texttip{\ge}{greater than or equal to} 4$ may or may not have an incircle. If it has an incircle, that is, it is possible to draw a circle such that all the sides of the polygon are tangents to the circle, then the above formula is applicable for the polygon also, which is:

$Area\ of\ the\ polygon = Semiperimeter \times Inradius$

-----------book page break-----------

Corollary-5

For a rightangled triangle with sides of length $a,\ b,\ c$, the length of the inradius $r$ can be found using the relation:

$r = \dfrac{1}{2} \times (a + b - c)$ where $c$ is the hypotenuse of the triangle.

In the following figure, $\triangle ABC$ is right-angled at $C$. Bisectors of $\angle A$ and $\angle C$ to intersect at $I$, which is the incentre of the triangle. $IP$, $IQ$ and $IR$ are the perpendiculars drawn from the incentre to the sides $AB$, $BC$ and $CA$ respectively.

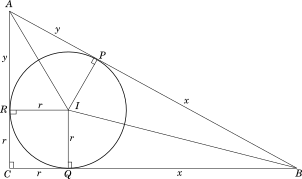
$IR$ and $IQ$ are perpendiculars to $AC$ and $BC$, and each is equal to $r$, therefore $IQCR$ is a square of side $r$

$\triangle IQB \cong IPB$,

$\therefore BQ = BR = x$

Similarly $AP = AR = y$

Therefore, the hypotenuse $c = x + y$

-----------book page break-----------

The sum of the other two sides is

$a + b = (r + x) + (r + y)$

$\Rightarrow a + b = 2r + x + y$

$\Rightarrow a + b - (x + y) = 2r$

Substituting $x + y = c$ we get:

$\Rightarrow a + b - c = 2r$

$\Rightarrow r = \dfrac{1}{2} \times (a + b - c)$