Incircle And Corner Circles Of A Triangle
$\underline{Theorem:}$
If $\Omega$ is the an incircle of $\triangle ABC$, and $\omega _A$, $\omega _B$ and $\omega_C$ are three circles touching $\Omega$ and two sides adjacent to each of the three vertices of the triangle, then their radii are related by:
$r = \sqrt{r_A\cdot r_B} + \sqrt{r_B\cdot r_C} + \sqrt{r_C\cdot r_A}$
where,
$r$, $r_A$, $r_B$ and $r_C$ are the radii of $\Omega$, $\omega_A$, $\omega_B$ and $\omega_C$ respectively.
$\underline{Construction:}$
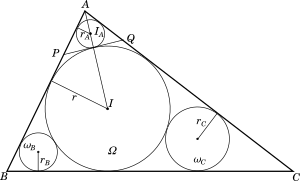
We draw $\triangle ABC$ with incenter $I$. We draw the tangent $PQ$at the contact point of $\Omega$ with $\omega_A$. Angle bisector $AI$ is drawn and the radii of the four circles are drawn as shown below. Let $I_A$ be the center of the circle $\omega_A$.
-----------book page break-----------
$\underline{Proof}$
Since $I_A$ is the incenter of $\triangle APQ$ it lies on the bisector of $\angle A$, similarly, since $I$ is the incenter of $\triangle ABC$ it also lies on the bisector of $\angle A$, therefore, $A$, $I_A$ and $I$ are colinear.
$\dfrac{r_A}{AI_A} = \dfrac{r}{AI} = Sin \dfrac{A}{2}$
$\Rightarrow \dfrac{r}{AI_A + r_A + r} = Sin\dfrac{A}{2}$
$\Rightarrow r = AI_ASin \dfrac{A}{2} + (r + r_A)Sin \dfrac{A}{2}$
$\Rightarrow r= r_A + (r+r_A)Sin \dfrac{A}{2}$
$\Rightarrow r - rSin \dfrac{A}{2} = r_A + r_ASin \dfrac{A}{2}$
$\Rightarrow r_A = r\left(\dfrac{1 - Sin \dfrac{A}{2}}{1 + Sin \dfrac{A}{2}}\right)$
Similarly,
$\Rightarrow r_B = r\left(\dfrac{1 - Sin\dfrac{B}{2}}{1 + Sin \dfrac{B}{2}}\right)$
-----------book page break-----------
Therefore,
$\sqrt{r_A\cdot r_B}$
$= r \times \sqrt{\dfrac{\left(1 - Sin\dfrac{A}{2}\right)\left(1 - Sin\dfrac{B}{2}\right)}{\left(1 + Sin\dfrac{A}{2}\right)\left(1 + Sin\dfrac{B}{2}\right)}}$
$= r \times \sqrt{\dfrac{\left(1 - Sin^2\dfrac{A}{2}\right)\left(1 - Sin^2\dfrac{B}{2}\right)}{\left(1 + Sin\dfrac{A}{2}\right)^2\left(1 + Sin\dfrac{B}{2}\right)^2}}$
$= r \times \sqrt{\dfrac{Cos^2\dfrac{A}{2} \cdot Cos^2\dfrac{B}{2}}{\left(1 + Sin\dfrac{A}{2}\right)^2\left(1 + Sin\dfrac{B}{2}\right)^2}}$
$= r \times \dfrac{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2}}{\left(1 + Sin\dfrac{A}{2}\right)\left(1 + Sin\dfrac{B}{2}\right)}$
We know that
$Cos^2x = 1 - Sin^2x$
$\Rightarrow \dfrac{Cos(x)}{1+Sin(x)} =\dfrac{1 - Sin(x)}{Cos(x)}$
-----------book page break-----------
Using the above relationship, we get:
$\sqrt{r_A\cdot r_B} = r \times \dfrac{\left(1 - Sin\dfrac{A}{2}\right)\left(1 - Sin\dfrac{B}{2}\right)}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2}}$
For the sake of brevity let us denote:
$Sin\dfrac{\theta}{2} = s_\theta$ and $Cos\dfrac{\theta}{2} = c_\theta$ for any angle $\theta$
which gives us:
$\sqrt{r_A\cdot r_B} = r \times \dfrac{\left(1 - s_A\right)\left(1 - s_B\right)}{c_A \cdot c_B}$
Therefore,
$\sqrt{r_A\cdot r_B} + \sqrt{r_B\cdot r_C} + \sqrt{r_C\cdot r_A}$
$= r \times \left\{\dfrac{\left(1 - s_A\right)\left(1 - s_B\right)}{c_A \cdot c_B} + \dfrac{\left(1 - s_B\right)\left(1 - s_C\right)}{c_B \cdot c_C} + \dfrac{\left(1 - s_C\right)\left(1 - s_A\right)}{c_C \cdot c_A}\right\}$
$= r \times \left\{\dfrac{\left(1 - s_A\right)\left(1 - s_B\right)\cdot c_C}{c_A \cdot c_B \cdot c_C} + \dfrac{\left(1 - s_B\right)\left(1 - s_C\right)\cdot c_A}{c_A \cdot c_B \cdot c_C} \right.$
$\left.+ \dfrac{\left(1 - s_C\right)\left(1 - s_A\right)\cdot c_B}{c_A \cdot c_B \cdot c_C}\right\}$
$= r \times \left\{\dfrac{c_C - s_Ac_C - s_Bc_C + s_As_Bc_C}{c_A \cdot c_B \cdot c_C} + \dfrac{c_A - s_Bc_A - s_Cc_A + s_Bs_Cc_A}{c_A \cdot c_B \cdot c_C} \right.$
$\left. + \dfrac{c_B - s_Cc_B - s_Ac_B + s_Cs_Ac_B}{c_A \cdot c_B \cdot c_C}\right\}$
-----------book page break-----------
$\dfrac{A}{2} + \dfrac{B}{2} + \dfrac{C}{2} = 90^\circ$
$\Rightarrow \dfrac{A}{2} + \dfrac{B}{2} = 90^\circ - \dfrac{C}{2}$
$\Rightarrow Sin \left(\dfrac{A}{2} + \dfrac{B}{2}\right) = Sin \left(90^\circ - \dfrac{C}{2}\right)$
$\Rightarrow Sin \dfrac{A}{2} Cos \dfrac{B}{2} + Cos \dfrac{A}{2}Sin \dfrac{B}{2} = Cos \dfrac{C}{2}$
Using the previously defined notations, the above identity can be written as:
$s_Ac_B + c_As_B = c_C$
Similarly, we can get:
$s_Bc_C + c_Bs_C = c_A$ and $s_Cc_A + c_Cs_A = c_B$
We get:
$\sqrt{r_A\cdot r_B} + \sqrt{r_B\cdot r_C} + \sqrt{r_C\cdot r_A}$
$= r \times \left\{\dfrac{s_As_Bc_C + s_Bs_Cc_A + s_Cs_Ac_B}{c_A \cdot c_B \cdot c_C}\right\}$
$= r \times \left\{\dfrac{Sin\dfrac{A}{2} Sin\dfrac{B}{2} Cos\dfrac{C}{2} + Sin\dfrac{B}{2} Sin\dfrac{C}{2} Cos\dfrac{A}{2} + Sin\dfrac{C}{2} Sin\dfrac{A}{2} Cos\dfrac{B}{2}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right\}$
$= r \times \left\{\dfrac{Sin\dfrac{B}{2} \left(Sin\dfrac{A}{2} Cos\dfrac{C}{2} + Sin\dfrac{C}{2} Cos\dfrac{A}{2}\right) + Sin\dfrac{C}{2} Sin\dfrac{A}{2} Cos\dfrac{B}{2}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right\}$
-----------book page break-----------
$= r \times \left\{\dfrac{Sin\dfrac{B}{2} Sin\left(\dfrac{A}{2} + \dfrac{C}{2} \right) + Sin\dfrac{C}{2} Sin\dfrac{A}{2} Cos\dfrac{B}{2}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right\}$
$= r \times \left\{\dfrac{Sin\dfrac{B}{2} Sin\left(90^\circ - \dfrac{B}{2} \right) + Sin\dfrac{C}{2} Sin\dfrac{A}{2} Cos\dfrac{B}{2}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right\}$
$= r \times \left\{\dfrac{Sin\dfrac{B}{2} Cos\dfrac{B}{2} + Sin\dfrac{C}{2} Sin\dfrac{A}{2} Cos\dfrac{B}{2}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right\}$
$= r \times \left\{\dfrac{Cos\dfrac{B}{2}\left(Sin\dfrac{B}{2} + Sin\dfrac{C}{2} Sin\dfrac{A}{2}\right)}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right\}$
$= r \times \left[\dfrac{Cos\dfrac{B}{2}\left\{Sin\left(90^\circ - (\dfrac{A}{2} + \dfrac{C}{2})\right) + Sin\dfrac{C}{2} Sin\dfrac{A}{2}\right\}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right]$
-----------book page break-----------
$= r \times \left[\dfrac{Cos\dfrac{B}{2}\left\{Cos(\dfrac{A}{2} + \dfrac{C}{2}) + Sin\dfrac{C}{2} Sin\dfrac{A}{2}\right\}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right]$
$= r \times \left[\dfrac{Cos\dfrac{B}{2}\left\{Cos\dfrac{A}{2}Cos\dfrac{C}{2} - \cancel{Sin\dfrac{A}{2}Sin\dfrac{C}{2}} + \cancel{Sin\dfrac{C}{2} Sin\dfrac{A}{2}}\right\}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right]$
$= r \times \left[\dfrac{Cos\dfrac{B}{2} \cdot Cos\dfrac{A}{2} \cdot Cos\dfrac{C}{2}}{Cos\dfrac{A}{2} \cdot Cos\dfrac{B}{2} \cdot Cos\dfrac{C}{2}}\right]$
$= r$