Introduction To Derivatives
I. Introduction To Derivative
Take a look at the curve of some function $y = f(x)$ shown below. Let us try to answer the question "What is the slope of the curve at point $P$?"
Let us say the coordinates of $P$ is given by $(x, f(x))$
If we select another point $Q$ at a horizontal distance $\Delta x$ away from $P$, the point $Q$ will have the coordinates $\left(x + \Delta x, f(x + \Delta x)\right)$.
-----------book page break-----------
Therefore, the slope, $s$, of the line $PQ$ in the above widget will be:
$s =$
$ \dfrac{f(x + \Delta x) - f(x)}{(x + \Delta x) - x} = \dfrac{f(x + \Delta x) - f(x)}{\Delta x}$
.Now, keeping the point $P$ fixed, try dragging the point $Q$ to bring it as close as possible to $P$. You will observe that as the point $Q$ comes closer and closer to $P$, the slope of $PQ$ will approach the slope of the tangent, and the line $PQ$ will almost coincide with the tangent. (You can try this for multiple points on the given curve by moving the point $P$).
We will get the exact value of the slope of the tangent, when the point $Q$ comes infinitesimally close to point $P$. As the point $Q$ approaches $P$ the value of $\Delta x$ becomes infinitesimally close to $0$.
Applying the concept of , we can say:
$s = \lim\limits_{\Delta x \rightarrow 0} \dfrac{f(x + \Delta x) - f(x)}{\Delta x}$
The above relationship is defined as the derivative of the function $f(x)$ with respect to $x$. Using mathematical notations, the derivative of a function $f(x)$ is denoted using $\dfrac{d}{dx}f(x)$ or $f'(x)$
Expressed in words, the derivative of a function with respect to a variable, is the ratio of the change in the value of the function to that of an infinitesimal change in the variable itself. The process of finding the derivative is called differentiation. We can see that the derivative of a function can also be a function itself, which can be differentiated again.
-----------book page break-----------
This will be called the second derivative of the function and will be denoted by $\dfrac{d^2}{dx^2}f(x)$ or $f''(x)$ or (occasionally) $f^2(x)$
Similarly, the $n\xasuper{th}$ derivative, when exists, can be denoted using $\dfrac{d^n}{dx^n} f(x)$ or $f^n(x)$
Now, let us try the following problem:
--------- Reference to question: fc397c3f-17cc-4563-bebc-7c2ff51f6683 ---------
-----------book page break-----------
II. Differentiability Of Functions
For a function $y = f(x)$ to be differentiable at $x = a$, we need:
$\lim\limits_{\Delta x \rightarrow 0^-} \dfrac{f(a + \Delta x) - f(a)}{\Delta x} = \lim\limits_{\Delta x \rightarrow 0^+} \dfrac{f(a + \Delta x) - f(a)}{\Delta x}$
Here,
$\lim\limits_{\Delta x \rightarrow 0^-} \dfrac{f(a + \Delta x) - f(a)}{\Delta x}$ is called the left side derivative of $f(x)$ at $x = a$, denoted by ${f'}_{-}(a)$ and
$\lim\limits_{\Delta x \rightarrow 0^+} \dfrac{f(a + \Delta x) - f(a)}{\Delta x}$ is called the right side derivative of $f(x)$ at $x = a$, denoted by ${f'}_{+}(a)$
We will take a couple of examples to understand this better.
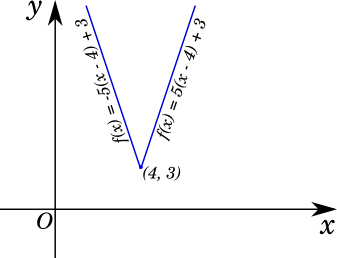
Let $f(x) = 5|x - 4| + 3$
We can write the function $f(x)$ as a union of two functions,
$f(x) =$
$\left\{ \begin{array}{ll} -5(x - 4) + 3, & \text{for } x < 4 \\ 5(x - 4) + 3, & \text{for } x \geqslant 4\end{array}\right.$
Therefore,
${f'}_{-}(4)$
$= \lim\limits_{\Delta x \rightarrow 0} \dfrac{-5(4 + \Delta x - 4) + 3 - (-5(4 - 4) + 3)}{\Delta x}$
$= \lim\limits_{\Delta x \rightarrow 0} \dfrac{-5 \Delta x}{\Delta x} = -5$
-----------book page break-----------
Similarly,
${f'}_{+}(4)$
$= \lim\limits_{\Delta x \rightarrow 0} \dfrac{5(x + \Delta x - 4) + 3 - 5(x - 4) - 3}{\Delta x}$
$= \lim\limits_{\Delta x \rightarrow 0} \dfrac{5 \Delta x}{\Delta x}$
$= 5$
Therefore, $f'(x)_{x = 4}$ does not exist, that is, $f(x)$ is not differentiable at $x = 4$
The following graph of $f(x)$ should clarify this concept more.
-----------book page break-----------
The graph of $f(x)$ to the left of $x = 4$ is a straight line, with a constant slope of $-5$ and the graph to the right of $x = 4$ has a constant slope of $5$. However, it is intuitive to see that at the point $x = 4$ it is impossible to find the slope since it is the intersection point of two lines, and the slope at this point is undefined.
Intuitively, we could say that if at any point of a curve there is a sharp intersection, the curve is not differentiable at that point.
Now try the following example:
--------- Reference to question: f150521a-6c32-4913-8413-818f2a06d0d6 ---------
As a formal definition of differentiability, we can say that a function $f(x)$ is differentiable at $x = a$, the function needs to fulfill two conditions:
1. The function $f(x)$ must be continuous at $x = a$.
2. The left derivative ${f'}_{-}(a)$ must be equal to the right derivative ${f'}_{+}(a)$
III. General Rules Of Differentiation
If $f(x)$ and $g(x)$ are two differentiable functions, and $k$ is a constant, then the following rules apply..
$i)\ \dfrac{d}{dx}k = 0$
$ii)\ \dfrac{d}{dx}[kf(x)] = k\dfrac{df(x)}{dx}$
-----------book page break-----------
$iii)\ \dfrac{d}{dx}[f(x) \pm g(x)] = \dfrac{d}{dx}f(x) \pm \dfrac{d}{dx}g(x)$
$iv)\ \dfrac{d}{dx} [f(g(x))] = \dfrac{d}{d[g(x)]} f(g(x)) \cdot \dfrac{d}{dx} g(x)$ $...\text{chain rule}$
$v)\ \dfrac{d}{dx}[f(x) \cdot g(x)] = g(x)f'(x) + f(x)g'(x)$ $...\text{product rule}$
$vi)\ \dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{g(x)f'(x) - f(x)g'(x)}{[g(x)]^2}$ $...\text{quotient rule}$
The first four of the above rules are trivial to understand and can be derived from the definition itself. Here we will see the derivation of the product rule and the quotient rule, and leave the derivation of the first three to the reader.
IV. Product Rule - Derivation
$\dfrac{d}{dx}[f(x) \cdot g(x)]$
$= $
$ \lim\limits_{\Delta x \rightarrow 0} \dfrac{f(x + \Delta x)g(x + \Delta x) - f(x)g(x)}{\Delta x}$
(by definition) Subtracting and adding $g(x+\Delta x)f(x)$ to the numerator, we get the limit as:
$\lim\limits_{\Delta x \rightarrow 0} \dfrac{f(x + \Delta x)g(x + \Delta x) - g(x+\Delta x)f(x) + g(x+\Delta x)f(x) - f(x)g(x)}{\Delta x}$
$= \lim\limits_{\Delta x \rightarrow 0} \dfrac{g(x + \Delta x)\{f(x + \Delta x) - f(x)\} + f(x)\{g(x+\Delta x) - g(x)\}}{\Delta x}$
$= \lim\limits_{\Delta x \rightarrow 0} g(x + \Delta x) \dfrac{f(x + \Delta x) - f(x)}{\Delta x} + \lim\limits_{\Delta x \rightarrow 0} f(x) \dfrac{g(x+\Delta x) - g(x)}{\Delta x}$
-----------book page break-----------
$= \lim\limits_{\Delta x \rightarrow 0} g(x + \Delta x) \lim\limits_{\Delta x \rightarrow 0} \dfrac{f(x + \Delta x) - f(x)}{\Delta x}$
$+ \lim\limits_{\Delta x \rightarrow 0} f(x) \lim\limits_{\Delta x \rightarrow 0} \dfrac{g(x+\Delta x) - g(x)}{\Delta x}$
$= \lim\limits_{\Delta x \rightarrow 0} g(x + \Delta x) \dfrac{df(x)}{dx} + f(x) \dfrac{dg(x)}{dx}$
$= g(x) \dfrac{df(x)}{dx} + f(x) \dfrac{dg(x)}{dx}$
V. Quotient Rule - Derivation
Here we will derive the quotient rule as stated before.
Let, $h(x) = \dfrac{f(x)}{g(x)}$ where $g(x) \ne 0$
$\Rightarrow f(x) = h(x)\cdot g(x)$
Differentiating both sides w.r.t $x$, and using the product rule from the previous section, we get:
$f'(x) = $
$g(x)h'(x) + h(x)g'(x)$
$\Rightarrow g(x)h'(x) = f'(x) - h(x)g'(x)$
$\Rightarrow h'(x) = \dfrac{f'(x) - h(x)g'(x)}{g(x)}$
$\Rightarrow h'(x) = \dfrac{f'(x) - \dfrac{f(x)}{g(x)}g'(x)}{g(x)}$
-----------book page break-----------
$\Rightarrow h'(x) = \dfrac{g(x)f'(x) - f(x)g'(x)}{[g(x)]^2}$
$\because h(x) = \dfrac{f(x)}{g(x)}$,
$h'(x) = \dfrac{d}{dx}\left[\dfrac{f(x)}{g(x)}\right] = \dfrac{g(x)f'(x) - f(x)g'(x)}{[g(x)]^2}$
Continuity Of Functions -