Linear Equations - Intercepts
$\underline{I.\ Understanding\ Intercepts}$
The intercepts of a linear equation are the points where a given straight line intersects the two axes. The $X$ intercept is the point where the line intersects the $X$ axis, and the $Y$ intercept is the point where the given line intersects the $Y$ axis. It is easy to understand that the point where a line intersects the $X$ axis will always have its $Y$ value as zero, and the point where it intersects the $Y$ axis, the $X$ value will be zero.
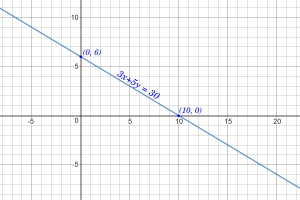
The given figure shows the equation of the line $3x + 5y = 30$
-----------book page break-----------
The line passes through the points $(10,\ 0)$ and $(0,\ 6)$. Both these points satisfy the given equation.
The intercepts of a given equation can be found using the following steps:
- Put $y=0$ in the equation, and then solve for $x$. This will give the value of the point which lies on the given equation as well as the $X$ axis.
- This is our $X$ intercept.
- Put $x=0$ in the equation, and then solve for $y$. This will give the value of the point which lies on the given equation as well as the $Y$ axis.
- This is our $Y$ intercept.
In a linear equation of the form $ax \pm by \pm c = 0$, if the constant $c = 0$, then the line passes through the origin and both the intercepts are $0$.
$\underline{Example\ 1:}$
We will take the line $3x + 5y = 30$ from our example above and find its intercepts
Putting $y = 0$ in the equation we get $3x = 30 \Rightarrow x = 10$, hence the $x$ intercept is $(10, 0)$
Putting $x = 0$ in the equation we get $5y = 30 \Rightarrow y = 6$, hence the $y$ intercept is $(0, 6)$
$\underline{Example\ 2:}$
Find the $X$ and $Y$ intercepts of the line $2x - 7y = 56$
Putting $y = 0$ in the equation we get $2x = 56 \Rightarrow x = 28$
Therefore, the $X$ intercept is $(28, 0)$
Again, putting $x = 0$ in the equation we get $-7y = 56 \Rightarrow y = -8$
Hence the $Y$ intercept of the line is $0, -8$
-----------book page break-----------
$\underline{II.\ Finding\ Equations\ From\ Intercepts}$
Now let us see how to represent an equation, given its $X$ and $Y$ intercepts.
If the $X$ intercept is $I_x$ and the $Y$ intercept is $I_y$, then the line can be represented as:
$\dfrac{x}{I_x} + \dfrac{y}{I_y} = 1$
It is very easy to see that if we put $x = 0$ in the above equation, we will get $y = I_y$ and if we put $y = 0$ we will get $x = I_x$
This line will pass through the points $(I_x, 0)$ and $(0, I_y)$, therefore, will have the given intercepts.
$\underline{Example 1:}$
Find the equation of the line whose $X$ and $Y$ intercepts are $-4$ and $7$ respectively.
We can directly replace the values of the two intercepts in the given form, to obtain the equation of the line.
Therefore, our equation is:
$\dfrac{x}{-4} + \dfrac{y}{7} = 1$ multiply both sides by $28$
$\Rightarrow -7x + 4y = 1$ changing sides appropriately we get:
$4y = 7x + 1$