Introduction To Trigonometric Ratios
We will start with our knowledge of similar triangles which we learnt .
$\underline{I.\ Basic\ Definitions}$
We know, that if two triangles $ABC$ and $PQR$ are similar with $\angle A = \angle P$, $\angle B = \angle Q$ and $\angle C = \angle R$, then the corresponding sides are in proportion, that is:
$\dfrac{AB}{PQ} = \dfrac{BC}{QR} = \dfrac{RP}{CA}$
To learn about trigonometric ratios we will consider two right triangles, and each with one angle equal to $\theta^\circ$ as shown in the following figure:
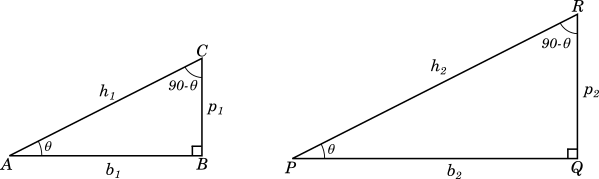
In the above triangles one angle of each is $90^\circ$ and the other one is $\theta$. Hence the third angle, for both, are $90 - \theta$. This means that the triangles are similar. The side opposite to the right angle is called the hypotenuse $(h)$, the side opposite to the angle $\theta$ is called the perpendicular $(p)$ and the non-hypotenuse side adjacent to angle $\theta$ is called the base $(b)$.
-----------book page break-----------
Since the triangles are similar, $\dfrac{p_1}{p_2} = \dfrac{b_1}{b_2} = \dfrac{h_1}{h_2}$.
Let us make a very important observation here, which is, no matter how large or small you draw either of the triangles, as long as the angle $\theta$ remains same, the above ratios will also remain the same.
So, we can say that the ratios of the sides of a right triangle are a function of one of the other angles.
Let us consider the equation:
$\dfrac{p_1}{p_2} = \dfrac{h_1}{h_2}$
$\Rightarrow \dfrac{p_1}{h_1} = \dfrac{p_2}{h_2}$
We can draw many more right triangles with the same base angle $\theta$ and obtain the same result, that is:
$\dfrac{p_1}{h_1} = \dfrac{p_2}{h_2} = \dfrac{p_3}{h_3} = ... = \dfrac{p_n}{h_n}$
Hence we can say that $\dfrac{p}{h} = constant$ for a right triangle as long as $\theta$ remains same.
Similarly if you take any ratio by selecting any two of the sides, $b$, $p$ and $h$, you can show that their ratio will remain constant as long as $\theta$ remains constant.
Mathematicians have given specific names to each of these ratios, and we will take a look at those names:
For example, the ratio $\dfrac{p}{h}$ is called $\unicode{0x201C}Sine\ of\ \theta\unicode{0x201D}$ and is written as $sin(\theta)$
The $\theta$ in bracket denotes that the ratio will change if $\theta$ changes, in other words the ratio of these two sides of the right triangle is a function of $\theta$ and is not dependent on any other factor like the size of the triangle.
-----------book page break-----------
Now let us take a look at the names of the other possible ratios:
The ratio $\dfrac{b}{h}$ is called $\unicode{0x201C}Cosine\ of\ \theta\unicode{0x201D}$ and is written as $cos(\theta)$
The following table lists the names of all the possible ratios, and the short form as they are written.
| Ratio | Name | Written As |
| $\dfrac{p}{h}$ | $Sine$ | $sin(\theta)$ |
| $\dfrac{b}{h}$ | $Cosine$ | $cos(\theta)$ |
| $\dfrac{p}{b}$ | $Tangent$ | $tan(\theta)$ |
| $\dfrac{h}{p}$ | $Cosecant$ | $cosec(\theta)$ |
| $\dfrac{h}{b}$ | $Secant$ | $sec(\theta)$ |
| $\dfrac{b}{p}$ | $Cotangent$ | $cot(\theta)$ |
-----------book page break-----------
$\underline{II.\ Inverses\ Of\ Ratios}$
Now let us look at some basic relationship between these ratios:
$sin(\theta) = \dfrac{p}{h} = \dfrac{1}{\dfrac{h}{p}} = \dfrac{1}{cosec(\theta)} \Rightarrow sin(\theta) \times cosec(\theta) = 1$
That is, $sin(\theta)$ and $cosec(\theta)$ are multiplicative inverses of each other.
Similarly,
$cos(\theta) = \dfrac{b}{h} = \dfrac{1}{\dfrac{h}{b}} = \dfrac{1}{sec(\theta)} \Rightarrow cos(\theta) \times sec(\theta) = 1$
Hence, $cos(\theta)$ and $sec(\theta)$ are multiplicative inverses of each other.
$tan(\theta) = \dfrac{p}{b} = \dfrac{1}{\dfrac{b}{p}} = \dfrac{1}{cot(\theta)} \Rightarrow tan(\theta) \times cot(\theta) = 1$
Hence, $tan(\theta)$ and $cot(\theta)$ are multiplicative inverses of each other.
-----------book page break-----------
$\underline{III.\ Complementary\ Ratios}$
Now, let us consider $\triangle ABC$ from the first figure, and name $\angle C$, with magnitude $90 - \theta$ as $\phi$. We have also rotated the triangle $90^\circ$ clockwise for better understanding.
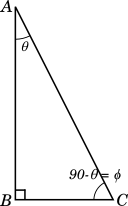
If we want to find the trigonometric ratios of $\phi$, then $AB$ will be the perpendicular (side opposite to $\angle C$), $CB$ will become the base and $AC$ will remain the hypotenuse.
$sin(\phi) = \dfrac{AB}{AC}$. We know that $\dfrac{AB}{AC} = cos(\theta)$
$\therefore sin(\phi) = cos(\theta)$
$\because \phi = 90 - \theta \Rightarrow sin(90 - \theta) = cos(\theta)$
Similary, $cos(90 - \theta) = cos(\phi) = \dfrac{BC}{AC} = sin(\theta)$
$tan(90 - \theta) = tan(\phi) = \dfrac{AB}{BC} = cot(\theta)$
-----------book page break-----------
$cosec(90 - \theta) = cosec(\phi) = \dfrac{AC}{AB} = sec(\theta)$
$sec(90 - \theta) = sec(\phi) = \dfrac{AC}{BC} = cosec(\theta)$
FInally, we will list all the ratios, along with their inverses and complementary ratios, in the following table:
| $sin(\theta) = \dfrac{1}{cosec(\theta)} = cos(90 - \theta)$ |
| $cos(\theta) = \dfrac{1}{sec(\theta)} = sin(90 - \theta)$ |
| $tan(\theta) = \dfrac{1}{cot(\theta)} = cot(90 - \theta)$ |
| $cosec(\theta) = \dfrac{1}{sin(\theta)} = sec(90 - \theta)$ |
| $sec(\theta) = \dfrac{1}{cos(\theta)} = cosec(90 - \theta)$ |
| $cot(\theta) = \dfrac{1}{tan(\theta)} = tan(90 - \theta)$ |