Limits Of Basic Trigonometric Functions

Here we will see the derivation of limits involving trigonometric functions that are important and useful in solving many other problems related to limits involving more complex trigonometric functions.

I. $\lim\limits_{\theta \rightarrow 0} \dfrac{\sin \theta}{\theta} = 1$

We will use a sector of a unit circle ($r = 1$) as shown in the following figure for this proof.

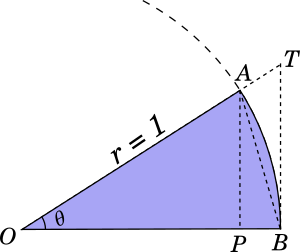
Let circle $\Omega$, with a radius $1$ unit, be centered at $O$. We draw the sector $AOB$ (shown in blue) in the above figure. Let the tangent at $B$ meet the extended radius $OA$ at $T$ and let $AP$ be the perpendicular dropped from $A$ to $OB$.

Let $\theta$ be the magnitude of $\angle AOB$ in radians.

$\tan \theta = \dfrac{TB}{OB} = \dfrac{TB}{1} = TB$

$\sin \theta = \dfrac{AP}{OA} = \dfrac{AP}{1} = AP$

$[\triangle AOB] = \dfrac{1}{2} AP \times OB = \dfrac{1}{2} AP = \dfrac{1}{2} \sin \theta$

$[\triangle TOB] = \dfrac{1}{2} TB \times OB = \dfrac{1}{2} TB = \dfrac{1}{2} \tan \theta$

$[sector AOB] = \dfrac{\theta}{2 \pi} \times \pi r^2 = \dfrac{\theta}{2}$

$[\triangle AOB] \ngtr [sector AOB] \ngtr [\triangle TOB]$

$\therefore [\triangle AOB] \le [sector AOB] \le [\triangle TOB]$

$\Rightarrow \dfrac{1}{2} \sin \theta \le \dfrac{\theta}{2} \le \dfrac{1}{2} \tan \theta$

$\Rightarrow \sin \theta \le \theta \le \tan \theta$

$1 \le \dfrac{\theta}{\sin \theta} \le \dfrac{1}{\cos \theta}$

Taking reciprocals of the above inequalities, we get:

$1 \ge \dfrac{\sin \theta}{\theta} \ge \cos \theta$

Taking limits of all the functions as $\theta \rightarrow 0$

$\lim\limits_{\theta \rightarrow 0} 1 \ge \lim\limits_{\theta \rightarrow 0} \dfrac{\sin \theta}{\theta} \ge \lim\limits_{\theta \rightarrow 0} \cos \theta$

Now, $\lim\limits_{\theta \rightarrow 0} \cos \theta$ is clearly equal to $1$, since $\cos 0 = 1$

$\therefore 1 \ge \lim\limits_{\theta \rightarrow 0} \dfrac{\sin \theta}{\theta} \ge 1$

The above inequality is only possible if $\lim\limits_{\theta \rightarrow 0} \dfrac{\sin \theta}{\theta} = 1$

II. $\lim\limits_{\theta \rightarrow 0} \dfrac{1 - \cos\theta}{\theta} = 0$

This limit can be derived easily using the previous limit we saw.

$\lim\limits_{\theta \rightarrow 0} \dfrac{1 - \cos\theta}{\theta}$

$= \lim\limits_{\theta \rightarrow 0} \dfrac{1 - \cos^2{\dfrac{\theta}{2}} + \sin^2{\dfrac{\theta}{2}}}{\theta}$

$= \lim\limits_{\theta \rightarrow 0} \dfrac{2\sin^2{\dfrac{\theta}{2}}}{\theta}$

$= \lim\limits_{\theta \rightarrow 0} \dfrac{\sin^2{\dfrac{\theta}{2}}}{\dfrac{\theta}{2}}$

$= \lim\limits_{\phi \rightarrow 0} \dfrac{\sin^2{\phi}}{\phi}$

$= \lim\limits_{\phi \rightarrow 0} \left( \dfrac{\sin{\phi}}{\phi} \times \sin\phi \right)$

$= \lim\limits_{\phi \rightarrow 0} \left( \dfrac{\sin{\phi}}{\phi}\right) \times \lim\limits_{\phi \rightarrow 0}\left( \sin\phi \right)$