Congruent Triangles

The word $\unicode{0x201C}Congruent\unicode{0x201D}$ means can be superimposed on one another, in other words matching exactly in size and shape.

Two triangles would match exactly when there is some way that you can place one triangle on top of another so that the three vertices would be falling exactly on top of each other and the triangles would appear as one. Let us try to get a feel of what congruency is.

Take a look at the figure below with $\triangle ABC$ and $\triangle PQR$

We can map vertex $P$ to vertex $A$, vertex $R$ to vertex $B$ and vertex $Q$ to vertex $C$. When we do, that you will be able to see only one triangle, with all points on $\triangle PQR$ falling on $\triangle ABC$. So, we can say the $\triangle ABC$ is congruent to $\triangle PQR$. Like we use the mathematical symbol $=$ for equality, for congruency we use the symbol $\texttip{\cong}{congruent to}$. That is an equal to sign, with a small wave (called tilde) on top.

Using mathematical symbol, we can write,

$\triangle ABC \texttip{\cong}{congruent to} \triangle PQR$

-----------book page break-----------

Let's take a look at another example below, with $\triangle DEF$ and $\triangle XYZ$.

We can map vertices $X$ to $F$, $Y$ to $D$ and $Z$ to $E$. Once we have done that, all parts of the two triangles will match exactly.

So, we can say that $\triangle DEF \texttip{\cong}{congruent to} \triangle XYZ$.

Let us take a look at another example, as shown in the following figure with $\triangle$s $ABC$ and $XYZ$, where $XYZ$ is an obtuse angled triangle and $ABC$ is acute angle triangle.

-----------book page break-----------

You can see that there is no way of mapping all three vertices of $\triangle XYZ$ on the three vertices of $\triangle ABC$. So we can say:

$\triangle ABC \ncong \triangle XYZ$ (Like $\neq$ means not equal to, $\ncong$ means not congruent to)

We will look at the various congruency rules in the subsequent sections.

II. Three Sided (SSS):

Suppose we were to draw a $\triangle PQR$ with $PQ = 6\ cm$, $QR = 5\ cm$ and $RP = 4\ cm$. How are we going to go about it?

We will first draw a line segment with any one of the lengths, lets take $PQ$ and make it $6\ cm$. Then with $P$ as center and $4\ cm$ radius we will draw and arc, and then with $Q$ as center and with $5\ cm$ as radius we will draw another arc to intersect the previous arc at the point $R$. We will get our triangle.

-----------book page break-----------

Can you think of a different triangle in a different way, that meets the same conditions. Of course, you can draw the point $R$ on the other side of the line $PQ$ but that will only be a reflection of this triangle. but it will not be a different triangle.

We will get the same triangle, even if we choose to draw the lines in a different sequence.

So, when you draw two triangles using the same side lengths, the triangles are exactly same. That is why, $SSS$ is a sufficient condition for congruency.

III. Two Sides And Included Angle (SAS):

Let us say we have to draw a $\triangle ABC$ with $AB = 5\ cm$, $BC = 3\ cm$ and the included $\angle ABC$ is $45^\circ$. How can we draw this? We can draw a straight line then draw an angle of $45^\circ$ on either side of the line. Mark this point as $B$. Then with $B$ as the center and a radius of $5\ cm$ draw an arc to intersect any one of the lines and let us call this point of intersection as $A$. With $3\ cm$ as radius and $B$ as center we draw another arc to intersect the other arm of our angle, let us call this intersection point $C$. You will observe that whichever line you choose to draw the $5\ cm$ and the $3\ cm$ arc, the triangle is going to be the same.

-----------book page break-----------

Given the lengths of any two sides and their included angle, we can draw only one unique triangle

Hence, any two triangles drawn with the same two sides and included angle are the same triangles.

Now, let us change the problem a little bit. Suppose we have two sides same and an angle which is not the included angle, will the triangles still be congruent? Let's try to draw a $\triangle PQR$ with $PQ = 5\ cm$, and $QR = 3\ cm$ and $\angle QPR = 45^\circ$.

Like before we will draw a line and an angle of $45^\circ$ at one end and call that point $P$. With $P$ as the center and a radius of $5\ cm$, we will cut a line segment of length $5 cm$ and call this point $Q$. To draw the line $QR = 3\ cm$ we will take $Q$ as the center and with $3\ cm$ radius will draw an arc to intersect the other line. As we see in the diagram below, this arc can intersect the other line at two different points. Both these points are at a distance of $3\ cm$ from $Q$. Joining $Q$ to any one of these points will give us a valid $\triangle PQR$ that meets the given criteria.

-----------book page break-----------

Therefore, given two sides and a non-included angle we can have two different triangles. So we cannot say that these two triangles are congruent.

IV. Two Angles And A Corresponding Sides (AAS):

Given two triangles $ABC$ and $PQR$, if we say that $BC = QR$ and $\angle ABC = \angle PQR$, and $\angle CBA = \angle PQR$, then we can say that the triangles are congruent. Let us take an example. Let us try to draw a $\triangle ABC$, with $BC = 6 cm$, $\angle ABC = 50^\circ$ and $\angle ACB = 60^\circ$.

We would take a line segment $BC = 6\ cm$, and draw an angle of $50^\circ$ at point $B$ and another angle of $60^\circ$ at point $C$. We will call the intersection point of these two arms of the new angles as $A$.

-----------book page break-----------

We will draw the $\triangle PQR$ in the same way. These two triangles will be exactly same, as shown below.

This triangle will fulfill the given conditions, and we can draw only one such triangle that fulfills the given condition. Suppose instead of the condition $\angle ACB = 60^\circ$, we were told that $\angle BAC = 70^\circ$, then also it would have been the same. Because given any two angles of a triangle, the third angle is always fixed. Remember, the triangles are congruent only if the corresponding angles are same.

-----------book page break-----------

If we change our example to say $BC = QR$, $\angle ABC = \angle PQR = 50^\circ$ and $\angle BCA = \angle QPR = 60^\circ$, then the triangles would not be congruent.

The angle corresponding to $\angle BCA$ is $\angle PRQ$ and while $\angle BCA = 60^\circ$ we can calculate that $\angle PRQ = 70^\circ$, hence the triangles are not congruent.

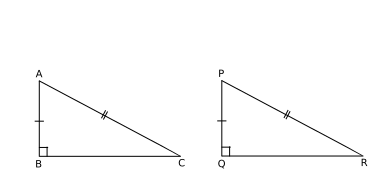
V. Hypotenuse And Any Side Of A Right Angled Triangle (RHS):

When we have two right angled triangles, with their hypotenuses and one other side equal the triangles are congruent.

-----------book page break-----------

Let us consider two triangles $\triangle ABC$ and $\triangle PQR$, as shown below, such that,

$\angle ABC = \angle PQR = 90^o$

$\overline{AB} = \overline {PQ} = 6\ cm$, and

$\overline{AC} = \overline{PR} = 10\ cm$ (the hypotenuse)

Let us see how they will be congruent. We will learn at a later stage that from Pythagorean Theorem, the square of the hypotenuse of a right angled triangle is equal to the sum of the squares of the other two sides.

In our example, for $\triangle ABC$

$AB^2 + BC^2 = AC^2$, therefore we can write:

$6^2 + BC^2 = 10^2$

$\texttip{\therefore}{therefore} BC^2 = 10^2 - 6^2 = 100 - 36 = 64$

$\texttip{\therefore}{therefore} BC = 8$.

Same way, for $\triangle PQR$

$PQ^2 + QR^2 = PR^2$

$6^2 + QR^2 = 10^2$

$QR^2 = 10^2 - 6^2 = 100 - 36 = 64$

$\texttip{\therefore}{therefore} QR = 8$

-----------book page break-----------

We can see, that if the hypotenuse and one other side is equal, the third side is also equal. We have seen in section $1$ that if all the $3$ sides of a triangle are equal, they are congruent. Therefore, if the hypotenuse and one other side of two triangles are equal, the third sides are also equal and they are congruent.